AFO 小技巧

编程思路

获得二进制前k位：a[i]&((1ll<<k)-1) ①；
若值域较大，可以通过建排名树状数组，避免离散化①；
维护单调队列的时候，如果已经存储了值，那么可以只记录下标，在维护的时候计算就好了②。
题目读入的时候使用的是字符串，每个字符表示一个 $16$ 进制下的数，而识别这个 $0\sim 9,\mathrm{A\sim F}$ 范围的字符，判断起来都要花很多行。我们可以直接 $\verb!string str=”0123456789ABCDEF”!$ ，对于字符 $c$ ，直接使用 $\verb!str.find(c)!$ ，返回的位置就是这个 $16$ 进制下的数。
状态压缩枚举 $S$ 以及它的子集每一个子集：（解释：S&T 的作用是保证 $T\in S$ ，每次减 $1$ 是枚举子集的操作）
code
```
For(S,1,(1<<n)) for(int T=S&(S-1);T;T=(T-1)&S) ...
```

做题思路

观察题目，观察题目条件、数据范围（手跑样例），猜测具体算法以及时间复杂度；
观察暴力分，思考如何打暴力分；
分析题目性质，这一点非常重要，往往是题目突破口，可以通过大样例获得思路；
不要放弃每一种思路，每次先手动模拟题目数据，观察题目性质③，观察有无能通过暴力模拟实现的方法（可以参看 $\text{CSP-S 2024 T2}$ ，我想得很复杂，实际就是模拟就好了），考虑枚举所有的情况，思维一定不能乱，每次要有条理的枚举④，再想这道题目对应的模板，考虑用模板解决问题，最后再想设动态规划转移；
写下具体思路，注重草稿，一定做到清晰明确，枚举所有的情况，防止挂题；
思考代码实现，按照思路写代码，每写完一段就打注释或者记录一段代码的意思，防止漏情况；
调题，验证时间复杂度，防止卡常，检查代码先从主函数入手，模板可以不用检查（一般模板是固定打法，不容易打错），判断代码实现是否满足所有的题目要求①。
再次回顾题目，重温所有条件并分析是否都适用所有性质。

小知识

$\verb!unique!$ 返回的是整理后第一个相同元素的位置。
$\verb!lower_bound!$ 返回的是第一个大于等于 $x$ 的位置，$\verb!upper_bound!$ 返回的是第一个大于 $x$ 的位置。$\verb!lower_bound!$ 在 $\verb!upper_bound!$ 前面，当 $x$ 不在数组中时，$\verb!lower_bound!$ 和 $\verb!upper_bound!$ 等价。
$\verb!s.erase(p1)!$并不会影响到其他关于 $s$ 的迭代器的遍历，且删除后再使用之前的迭代器遍历会直接跳过删除的值。
$\mathrm{STL}$ 容器访问最后的元素指针是 $\verb!s.rbegin()!$ ，不是 $\verb!s.cbegin()!$。$\verb!s.cbegin()!$ 是用来访问这个容器的只读模式下的 $\verb!s.begin()!$ ，$\verb!s.crbegin()!$ 是访问这个容器只读模式下的的 $\verb!s.rbegin()!$ ①。

一定注意！！！

检查数据范围，一道题最多花费 $40-50\ min$ 分析，每道题必须先手跑样例，做题前先加编译参数 -std=c++14 -O2 -Wl,--stack=1073741824 -Wall。可以使用 -ftrapv 检验是否出现爆 $\verb!long long!$ 的情况，注意不要和 -O2 参数同时开，否则会失效。
Linux 下记得使用 g++ -g test.cpp -o test -Wall -O2 -fsanitize=undefined,address 函数来检验程序，可以用 ./test 来运行程序。
并列的 if 判断后面没有写 else 导致前后判断相互影响。
$\mathrm{STL}$ 容器要先判断 $\verb!.empty()!$ 再引用。
注意inline input()， 一定要在 Linux 环境下验证。
注意图的连通性。
每次使用 (1<<i) 类似的语句的时候，考虑使用 (1ll<<i) 甚至 (1ull<<i) 来计算，防止出现数字越界。！
双指针的时候请注意边界，左端点一定要小于等于右端点！！！①
打代码前先枚举每一种情况，并写到电脑或者纸上，最后再进行代码实现④。
在如果代码同时写了暴力和正解，在不保证暴力正确性的情况下，不要交暴力，我就因为这个挂了 $60\text{pts}$ 。
关键字 y0,y1,yn,j0,j1,jn 是 C++ 的函数，因此使用的时候要避免用到这几个函数，但是每次在 Linux 下运行才是保证代码不出问题的最好方法。
在处理乘法逆元的时候，一定要注意判 $0$ ，建议这么打，**也可以直接令 inv[0]=1**：

inline int C(int n,int m){
    if(n==0 || m==0 || n<=m) return 1;
    return fac[n]*inv[m]%mod*fac[n-m]%mod;
}

struct 内定义数组的时候不要定义太大，特别是 pair<int,int> 数组，如果出现 out of memory allocating 65536 bytes ，可以在前面加一个 $\verb!int!$ 这个问题就解决了。

const int M = 501234;
struct LCA{
	P rev[M][20];//这样会报错
}G;

const int M = 501234;
struct LCA{
	int sbdevcpp;//这样就好了
	P rev[M][20];
}G;

卡常技巧

时间复杂度时尽量不要超过 $O(10^8)$ 。
卡常一定要在虚拟机下跑代码，这样跑出来才是最真实的，基本上 $0.5$ 秒内都能过，除非被出毒瘤数据。
建议写快读快输，对于所有题目使用这个就很快了。
clock()函数的返回值是根据编译器决定的，在 $\text{Windows}$ 系统下 $1s$ 的返回值是 $1000$ ，在 $\text{Linux}$ 系统下返回值是 $1000000$ ，因此，在使用这个函数的时候建议用 Tim = 1.*clock()/CLOCKS_PER_SEC 来表示实际时间（单位：$s$）。
可以使用 constexpr 参数替换 const ，所有静态的参量全部用 constexpr ，特别是 $\text{Hash}$ ，对常数的优化非常不错。注意 constexpr 不要定义在 struct 里面，且定义在结构体内的 const 会失效 ①。
线段树的 pushup() 操作如果传入的是结构体（例如 pushup(tr[p],tr[ls],tr[rs]); ），记得不要传入 $\mathrm{STL}$ 容器，否则时间复杂度至少增加 $3$ 倍以上⑤。
遇到 bool 就换成 bitset ，而且可以使用 vst._Find_first() 和 vst._Find_next(i) 函数，甚至可以用 vst.count() 来计算 $1$ 的个数。时间复杂度 $O(\frac{n}{w})$ ，$w$ 为电脑操作位数。
inline 和 register 没用，因为编译器开了 -O2 后优化地比你好。
vector 可以提前申请内存，使用 vec.reverve(n) 语句即可
多使用位运算，注意加括号。
注意访问的连续性，使用数组访问 a[0],a[1] 比 a[0],a[10001] 快得多。
更多技巧参考：浅论 OI 中的卡常技巧（基本完成）- 知乎

思维拓展

计算方案数时，可以以答案为下标进行考虑①。
当需要求解“删除”、“合并”、“添加”类题目时，考虑逆向操作②。
不要求强制在线就考虑离线处理：将询问离线，枚举右区间，运用树状数组维护，可以在 $O(nlogn)$ 时间内求出答案③；也可以使用莫队算法，处理比较复杂的区间问题④。
正解并不意味着就一定是所有情况的通解，也有可能是每种情况的解的总和④。
多重背包选择时，可以使用二进制优化枚举选几个当前物品。例如将可以选 $14$ 个的某种物品变成选 $7,4,2,1$ 个物品，转换为 $\mathrm{01}$ 背包来计算⑤。
双向搜索思想：当出现单向枚举或搜索代价是指数级时，考虑寻找中间点，先计算前面的，再计算后面的。例如例题中 $abcdcd$ ，每次枚举的代价都是 $O(S)$ （即字符种类数），单项枚举时间复杂度是 $O(nS^3)$ （ $n$ 是字符串长度），但是固定一个中间点 $c$ ，预处理出 $ab$ 的方案数和 $dcd$ 的方案数时间复杂度便降到了 $O(nS)$ ⑥。
由一般到特殊：优先寻找题目的特殊点，考虑能否将一般的计算转化为特殊的计算⑦。
由简单到复杂：将题目变成更简单的形式，把这个形式推理到更复杂的形式中⑧。
需求方与供应方的转换：如果要求多个对象的答案，枚举每个对象并分别计算它自己的贡献的代价很大，转换为考虑枚举每个能对询问对象产生贡献的点，计算这些贡献点对答案的贡献⑨。
容斥原理：很重要，不要忘了。
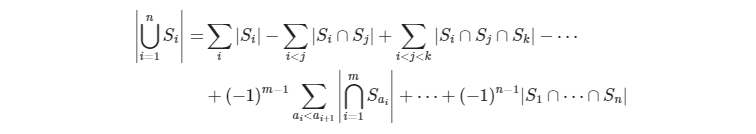
当前存在多种操作的时候，可以考虑先全部用一种操作，在考虑剩余操作对答案的影响⑩。
遇到数学公式计算的时候，一定要尝试推式子，然后观察规律①。
可以使用随机数来代表一个集合或者一个极大数的权值，把这个当成这个数的键值，实际就可以进行类似 Hash 的多个值比较，为了防止被卡，可以使用两个数分别记录异或和和加和，详见后面的 Hash 。

序列操作

区间询问处理：
1. 先思考能不能使用区间合并求值（区间合并可以使用 $O((n+q)\log n)$ 时间完成），
2. 否则就尝试使用莫队算法，根号分治（就是分块）来解决问题，
3. 也可以考虑将区间离线，固定右端点再使用树状数组处理询问。
有关序列的处理：
1. 求前缀和找规律；
2. 用下标乘上数值；
3. 数值范围允许时，考虑将下标和数值取反；
4. 前后做差找规律；
5. 将序列转化为统一的形式，例如将一段 $1111011000$ 看作 $4$ 个 $1$ 、$1$ 个 $0$ 、$2$ 个 $1$ 、$3$ 个 $0$ 的形式① ；
6. 遇到求 $01$ 串中 $1$ 比 $0$ 多的个数，可以把 $0$ 转换为 $-1$ ，通过前缀和求解②。
对序列进行操作：
1. 从小范围考虑到大范围；
2. 动态规划（可以多尝试几个 $f_{i,j}$）；
3. 从答案开始操作（逆向操作）；
4. 考虑将区间修改压缩到具体的一个点上③。
括号序列：
1. 用栈存储维护；
2. 动态规划处理子问题④。

动态规划

发现有任何值非常小且存在选与不选的问题时，考虑状态压缩① 。
$f[l][r]$ 可以表示区间 $[l,r]$ 的一些性质，其中 $l$ 和 $r$ 都表示下标②。
动态规划的状态数不只有一个，当发现有些东西很难求时，考虑直接使用 $\mathrm{dp}$ 求解③。
若发现当前状态会影响到未来的状态，考虑逆向操作④。
维度压缩：找到维度的相同点，统一即可⑤。
树形 $\text{dp}$ 一般定义 $f_{x,j}$ 表示以 $x$ 为根的子树的状态⑥。

哈希函数以及哈希表

这几天老是被卡双哈希，心态都给搞炸了。之后干脆用一个谁都不会去卡的 Hash 模数，陈列如下：
被卡记录
我双哈希又被卡了 [①](https://wolfdeer62456.github.io/2024/11/19/C241119A-%E5%AD%97%E7%AC%A6%E4%B8%B2/) 记录模数： `m1 = 998244353, b1 = 131` `m2 = 1e9+9, b2 = 997`

mod1 = 1e9+97, bas1 = 1333331;
mod2 = 998244991, bas2 = 997;
return (t1<<31)+t2;//这样最不容易被卡，相当于存了个pair

哈希集合：对于每一个集合中的元素（比如一个 __int128 类型的数字），随机一个在 $1\sim 1e9$ 之间的数，用这个数来表示这个元素的键值，维护两个值 $S_1$ 和 $S_2$ ，分别记录所有出现元素的加权和与异或和，防止出现重复。两个集合相等当且仅当它们对应的 $S_1$ 和 $S_2$ 相等①。

哈希表：使用 Hash 来模拟 $\verb!map!$ ，但是常数更小。可以使用链表法，创建邻接表，取一个合适的数，将每一个数对这个数取模，并且存在这个数对应的邻接表或 vector 中，每次遇到一个数直接暴力查询即可。注意哈希表清空的时间复杂度，使用邻接表只需要 memset 一个 $first$ 数组，但是使用 vector 就需要 $O(n)$ 复杂度。注意vector要放外面。

模板

使用 vector 解决：

const int M = 200;
struct Hash_List{
	vector<P> link[1024];
	inline int add(int x,int v=1){
		for(auto &p:link[x%M]) if(p.x==x) return p.y+=v;
		link[x%M].emplace_back(x,v);return v;
	}
	inline int chkins(int x,int v){
		for(auto &p:link[x%M]) if(p.x==x) return p.y;
		link[x%M].emplace_back(x,v);return v;
	}
	inline int operator[](int x){
		for(auto &p:link[x%M]) if(x==p.x) return p.y;
		return 0;
	}
	void clear(){For(i,0,M-1) link[i].clear();}
}mp,hsh,exi;

使用邻接表解决：

const int M = 800;
struct HL{
	int hd[805], nxt[N<<3|7], tot;
	int num[N<<3|7], sum[N<<3|7];
	inline int add(int x,int v=1){
		int tmp = x%M;
		for(int i=hd[tmp];i;i=nxt[i]) if(num[i]==x) return sum[i]+=v;
		nxt[++tot]=hd[tmp], hd[tmp] = tot;
		num[tot] = x, sum[tot] = v;return v;
	}
	inline int chkins(int x,int v){
		int tmp = x%M;
		for(int i=hd[tmp];i;i=nxt[i]) if(num[i]==x) return sum[i];
		nxt[++tot]=hd[tmp], hd[tmp] = tot;
		num[tot] = x, sum[tot] = v;return v;
	}
	inline int operator[](int x){
		int tmp = x%M;
		for(int i=hd[tmp];i;i=nxt[i]) if(num[i]==x) return sum[i];
		return 0;
	}
	inline void clear(){memset(hd,0,sizeof hd), tot=0;}
}mp,hsh,exi;

对环的处理

方法1： 枚举 $n$ 次断边，转化为 $n$ 条长度为 $n$ 的链，从 $n$ 个最小值中再取最小值①。
方法2： 复制一遍节点，转化为一条长度为 $2n$ 的链，从中选取长度为 $n$ 且分数最小的一段链。方法 $1$ 的时间复杂度会扩大 $n$ 倍，方法 $2$ 的时间复杂度只是原来的 $2$ 倍②。

出现gcd或lcm计算的思路

枚举质因数，对于 $[1,n]$ 范围，每次枚举质因数和其倍数，时间复杂度为 $O(n+\frac{n}{2}+\frac{n}{3}+\frac{n}{4}+…+1)=O(n\ln n)$ 。
集合里面加入数字后 $\gcd$ 若改变则至少除 $2$ ，所以长度为 $n$ 数组中不同的 $\gcd$ 数量最多 $O(n\log ⁡a)$ 级别，其中 $a$ 表示值域①。
对于每一个点 $l$ ，以之为区间的左边界，在端点从 $r$ 转移到 $r+1$ 时，$\gcd$ 要么不变，要么变化，因此，对于 $j\in [l,n]$ ，区间 $[l,j]$ 的 $\gcd$ 会随着 $j$ 的增长呈阶梯式下降趋势①。

出现二进制计算的思路

出现有边权的图或者树：1.按边权的进制位建边，当前点二进制表示下的第 $k$ 位如果为 $1$ ，就在 $2^k$ 的图上建边，最多建 $O(\log a)$ 张图①。
题目中有按位异或：1. 将答案分成 $\log A$ 份计算，每次分别处理 $[2^k,2^{k+1})$ 的答案②； 2. 两次异或同一个值对原数字没有影响；3. 考虑建 $\mathrm{Trie}$ 树处理问题③。
题目中有按位与：1.每次按位与后当前值一定变小，可以考虑二分。

出现mex计算的思路

找规律，大多数时候都会出现有特殊值的情况，这个时候直接分类讨论即可 ①。

乘法逆元

如果模数为质数，直接求 ksm(x,mod-2) 便能求出逆元。
如果模数是合数，可以观察当前模数的性质，例如 $1e9+6$ 可以分成 $5e8+3$ 和 $2$ 两个质数，可以先求出 $x$ 在 $mod=5e8+3$ 时的模数，最后在乘个 $2$ 即可①。

出现 n 为极大值

推 $\text{dp}$ 式子（一般为二维），用矩阵快速幂求解。
$n$ 可能为值域，考虑离散化①。
时间复杂度可能与 $n$ 无关或为 $\log n$ ②。

计算路径数量

双向搜索降低时间复杂度
枚举路径中间点，计算路径条数
求类似最短路问题，考虑在反图中计算最短路，再正向搜索 $\mathrm{dp}$ 转移①。

图论

图变树：
1. 最小生成树①；
2. $\text{Kruskal}$ 重构树；
3. 树上笛卡尔树（$\text{Kruskal}$ 重构树变形）③;
4. $\text{dfs}$ 搜索树④；
5. 单点最短路树⑤；
6. 圆方树⑥；
图变 $\text{DAG}$：
1. $\verb!tarjan!$ 缩点，重建 $ \text{DAG} $ ；
最短路算法
1. $\text{dijkstra}$ 变式：根据题目要求更换优先队列的键值；

树上操作

$n$ 个点的树， $q$ 次询问 $x$ 和 $k$ 输出点 $x$ 的 $k$ 级祖先，$n,q\le1e7$。考虑深搜，用栈存储祖先，离开后弹出。
$n$ 个点的树，每次随机删除一个点及其子树，求删完整棵树的期望，$n,q\le1e7$。由于每次删除一个点的贡献为 $1$ ，删除非祖先节点不会对当前点的贡献造成影响，因此当前点有贡献的概率就是在所有的祖先节点和自己中选到自己的概率，即 $\frac{1}{dep[x]}$，根节点的深度为 $1$ 。
遇见树上路径，考虑使用树上差分，甚至可以使用容斥原理④。
单点加、连查询转换为子树加、单点求和：考虑树上差分
树上路径 $\mathrm{xor}$ 的计算：令 $dis[x]$ 表示点 $x$ 到根的路径异或和，那么有 $\verb!f(x,y)=dis[x]^dis[y]!$ ，$\verb!f(x,y)!$ 表示 $x$ 到 $y$ 的路径异或和，可以通过这个性质求出每个点到根的路径异或和并建立 $\text{01Trie}$ 树，由此可求得树上最大异或路径和 ③。
树上路径 $\verb!&!$ 或 $\verb!|!$ 操作：建 $2^k$ 分层图②。
要求树上某个点是否在点 $x$ 的子树内，可以使用类似树链剖分的方法，记录每个点的 $\verb!dfn!$ 和 $\verb!siz!$ ，点 $y$ 在点 $x$ 的子树（含 $x$ ）内当且仅当 dfn[x]<=dfn[y] && dfn[y]<=dfn[x]+siz[x]-1 ①。
思维：遇见树链（关键点到跟）的并的问题的经典做法：