网址
题目详情 - 【NOIP模板】树链剖分 - LOJ模板 - Super
题解 - 【NOIP模板】树链剖分 - LOJ模板 - Super
题解
给你一棵有点权的树,开始时根为 1 号点,请你实现以下操作:
- 换根
- 一条链上点权加
- 一个子树内点权加
- 询问一条链上点权的和
- 询问一个子树内的点权和
操作大多数和模板题一样,且不用取模,但是多了一个换根操作。
所以对于链上的操作是不会影响的,只有子树部分操作有影响。
首先考虑暴力,每次换根后重构,那么复杂度显然接受不了,所以我们要考虑不重构,所以开始的时候就以一号点为根,先把树剖了,线段树建出来。
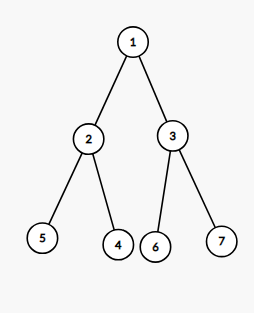
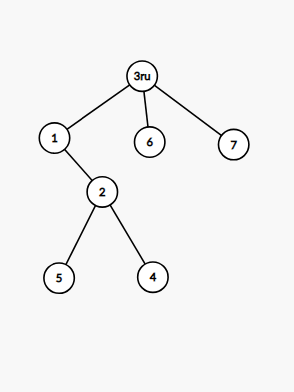
此时,我们就要考虑不同的根和子树操作该如何实现,我们假设根为 r,操作子树的根节点为 u,那么有如下几种情况(原来的子树是指的在根为 1 时的子树):
当 u=r,此时操作范围就是整个树,将整个树加或者求和即可。
 =>
=> 
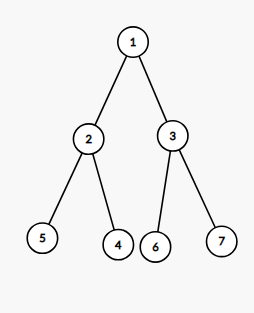
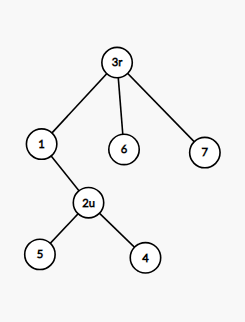
当 r 不在 u 的原来的子树里面时,操作范围就是原来的子树。
 =>
=> 
当 r 在 u 的子树内时,情况就比较复杂,操作范围就为整个树减去 u 到 r 路径上深度最小的点(不包含 u 点)的原来的子树。
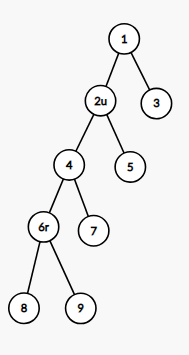 =>
=> 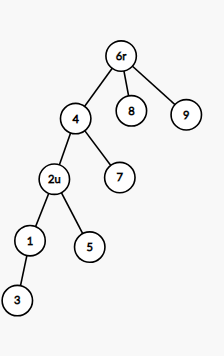
比如上面这个例子就是,我们现在 6 号点为根,查询 2 号点,它的子树就是 1,3,5,也就是原来的整个树减去 4 号点的原来的子树剩余部分,而 4 号点刚好是 6 ∼ 2 上不包含 2 的深度最小的点。
所以我们再子树操作的时候再稍微判断一下,分类讨论求一下就好啦,求路上深度最小的点可以倍增往上跳,也可以直接树剖的线段树维护即可。
#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int>
#define int long long
inline int rd(){int x;return cin>>x,x;}
const int N = 2012345;
bool ST;
int n,m,a[N],root=1;
vector<int> ft[N];
int son[N],siz[N],dep[N],fa[N];
void dfs_son(int x,int father){
siz[x]=1,dep[x]=dep[father]+1,fa[x]=father;
for(auto y:ft[x]){
if(y==father) continue;
dfs_son(y,x);
siz[x]+=siz[y];
son[x]=siz[son[x]]>=siz[y]?son[x]:y;
}
}
int top[N],w[N],id[N],cnt;
void dfs_top(int x,int tp){
top[x]=tp,id[x]=++cnt,w[cnt]=a[x];
if(!son[x]) return;
dfs_top(son[x],tp);
for(auto y:ft[x]){
if(y==fa[x]||y==son[x]) continue;
dfs_top(y,y);
}
}
#define mid ((l+r)>>1)
#define ls (p<<1)
#define rs (p<<1|1)
struct Tr{int sum,add,siz;}tr[N<<2|3];
void pushup(Tr &T,Tr L,Tr R){T.sum=L.sum+R.sum;}
void build(int p,int l,int r){
tr[p]={w[l],0,r-l+1};
if(l==r) return;
build(ls,l,mid),build(rs,mid+1,r);
pushup(tr[p],tr[ls],tr[rs]);
}
void pushdown(int p){
if(tr[p].add){
tr[ls].sum+=tr[ls].siz*tr[p].add;
tr[rs].sum+=tr[rs].siz*tr[p].add;
tr[ls].add+=tr[p].add;
tr[rs].add+=tr[p].add;
tr[p].add=0;
}
}
void update(int p,int l,int r,int L,int R,int k){
if(L<=l&&r<=R){
tr[p].sum+=tr[p].siz*k;
tr[p].add+=k;return;
}
pushdown(p);
if(L<=mid) update(ls,l,mid,L,R,k);
if(R>mid) update(rs,mid+1,r,L,R,k);
pushup(tr[p],tr[ls],tr[rs]);
}
inline Tr ask(int p,int l,int r,int L,int R){
if(L<=l&&r<=R) return tr[p];
pushdown(p);
if(R<=mid) return ask(ls,l,mid,L,R);
if(L>mid) return ask(rs,mid+1,r,L,R);
Tr T;return pushup(T,ask(ls,l,mid,L,mid),ask(rs,mid+1,r,mid+1,R)),T;
}
void update_path(int x,int y,int k){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
update(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
update(1,1,n,id[y],id[x],k);
}
void update_tree(int x,int k){
if(id[x]==id[root]) update(1,1,n,id[1],id[1]+siz[1]-1,k);else//x为根节点
if(id[x]<id[root]&&id[root]<=id[x]+siz[x]-1){//root在x子树中
update(1,1,n,id[1],id[1]+siz[1]-1,k);//先加上总数
int y=root;//从root开始跳
while(fa[top[y]]!=x && top[y]!=top[x])y=fa[top[y]];
if(fa[top[y]]==x) y=top[y];//root在x的轻链上
if(top[y]==top[x]) y=son[x];//root在x的重链上
update(1,1,n,id[y],id[y]+siz[y]-1,-k);
}
else{update(1,1,n,id[x],id[x]+siz[x]-1,k);}//root不在x子树中
}
int ask_path(int x,int y){
int res=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
res+=ask(1,1,n,id[top[x]],id[x]).sum;
x=fa[top[x]];
}
if(dep[x]<dep[y]) swap(x,y);
return res+ask(1,1,n,id[y],id[x]).sum;
}
int ask_tree(int x){
if(id[x]==id[root]) return ask(1,1,n,id[1],id[1]+siz[1]-1).sum;else
if(id[x]<=id[root]&&id[root]<=id[x]+siz[x]-1){
int res=ask(1,1,n,id[1],id[1]+siz[1]-1).sum;
int y=root;
while(fa[top[y]]!=x && top[y]!=top[x])y=fa[top[y]];
if(fa[top[y]]==x) y=top[y];
if(top[y]==top[x]) y=son[x];
return res-ask(1,1,n,id[y],id[y]+siz[y]-1).sum;
}else{return ask(1,1,n,id[x],id[x]+siz[x]-1).sum;}
}
bool ED;
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
cin>>n;For(i,1,n) cin>>a[i];
For(i,1,n-1){
int x=i+1,y;cin>>y;
ft[x].push_back(y);
ft[y].push_back(x);
}
dfs_son(root,0);
dfs_top(root,root);
build(1,1,n);
cin>>m;
while(m--){
int k = rd(),x,y,z;
switch(k){
case 1:{cin>>root;break;}
case 2:{cin>>x>>y>>z;update_path(x,y,z);break;}
case 3:{cin>>x>>y;update_tree(x,y);break;}
case 4:{cin>>x>>y;cout<<ask_path(x,y)<<'\n';break;}
case 5:{cin>>x;cout<<ask_tree(x)<<'\n';break;}
}
}
return 0;
}


