#C231108A. 最大公约数(gcd)
标签(Label)
- gcd
- 值域转下标
前言(Front talk)
$\qquad$我也不知道为什么这样打会是最优解,当时做题的时候我甚至还在思考 $O(n\sqrt{n})=3\times10^8$ 到底能不能过,结果这玩意儿 $40ms$ 就跑完了,我还搁哪想了半天更优解。( ̄_ ̄|||)
网址(Website)
题解(Solution)
$\qquad$讲一下倒着来做的做法,将每个 $a_i$ 放进一个值域里面(这道题 $a_i$ 的数据范围救了我),然后倒着寻找可能的最大 $gcd$ ,用 $sum$ 数组分别记录 $i$ 是 $a$ 数组中多少个数的约数,由于有 $k$ 的限制,我们用 $ma[i]$ 数组和 $mi[i]$ 数组来维护这些约数在 $a$ 数组中的最大位置和最小位置,如果 $sum[i]>=2$ 且 $ma[i]-mi[i]>=k$ 则 $i$ 可以作为最大的最大公约数,直接退出循环,输出即可。
$\qquad$实际上 $sum[i]$ 数组根本不用维护,因为如果 $i$ 当前只有一个,那么 $ma[i]$ 一定等于 $mi[i]$ ,不会满足 $ma[i]-mi[i]>=k$ 的条件,因为数据范围中 $k>=1$ 。
代码(Code)
我的代码
$\qquad$实际上速度比题解还快,因为不是严格 $O(n\sqrt{n})$ 的。
$\qquad$目前试出来最快是总共 $125ms$ ,相较于正解的 $1097ms$ 不知道优化了多少。
#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
char buf[100],*p1=buf,*p2=buf;
inline int gc(){ return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,100,stdin),p1==p2)?EOF:*p1++; }
inline int input(){
int x=0; char ch=gc(); bool f=1;
while(!isdigit(ch)) f^=ch=='-',ch=gc();
while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=gc();
return f?x:-x;
}
const int M = 1012345;
const int N = 301234;
int n,k,a[N];
bitset<M> hav;
int sum[N];
int ma[M],mi[M];
signed main(){
string str("gcd");
freopen((str+".in").c_str(),"r",stdin);
freopen((str+".out").c_str(),"w",stdout);
memset(mi,0x3f,sizeof(mi));
n=input(),k=input();For(i,1,n){
a[i]=input();
ma[a[i]]=max(ma[a[i]],i);
mi[a[i]]=min(mi[a[i]],i);
hav[M-a[i]]=true;
}int i,p,w;
for(i=hav._Find_first();M-i<=M;i=hav._Find_next(i)){
p=M-i;if(ma[p]-mi[p]>=k) return cout<<p<<'\n',0;
int q=(int)sqrt(p);
for(int j=2;j<=q;++j){
if(p%j==0){w=p/j;
ma[j]=max(ma[j],ma[p]);
mi[j]=min(mi[j],mi[p]);
ma[w]=max(ma[w],ma[p]);
mi[w]=min(mi[w],mi[p]);
hav[M-j]=true,hav[M-w]=true;
}
}
}return 0;
}题解代码
$\qquad$还是把题解的加上吧,题解是正着来的。
#include <iostream>
#include <cstdio>
#define maxn 1000000
using namespace std;
int n,k,a[300005];
int mn[1000005],mx[1000005];
int ans;
int main(){
freopen("gcd.in","r",stdin);
freopen("gcd.out","w",stdout);
scanf("%d%d",&n,&k);
for (int i=1;i<=maxn;i++)mn[i]=n+1,mx[i]=0;
for (int i=1;i<=n;i++){
scanf("%d",&a[i]);
mn[a[i]]=min(mn[a[i]],i);
mx[a[i]]=max(mx[a[i]],i);
}
for (int i=1;i<=maxn;i++){
int l=n+1,r=0;
for (int j=i;j<=maxn;j+=i){
l=min(l,mn[j]);
r=max(r,mx[j]);
}
if (r-l>=k)ans=i;
}
printf("%d\n",ans);
return 0;
}后续(Ending)
时间证明:
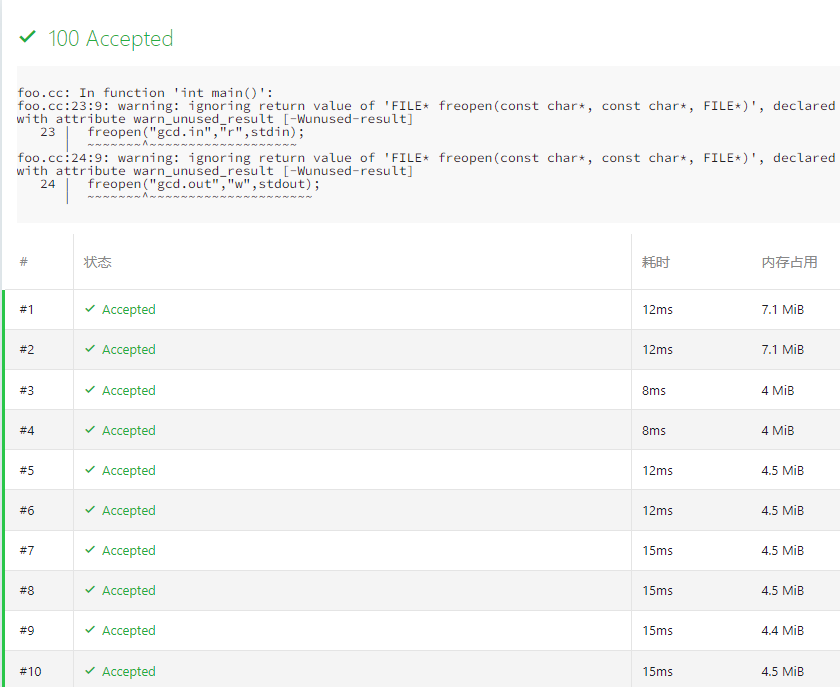

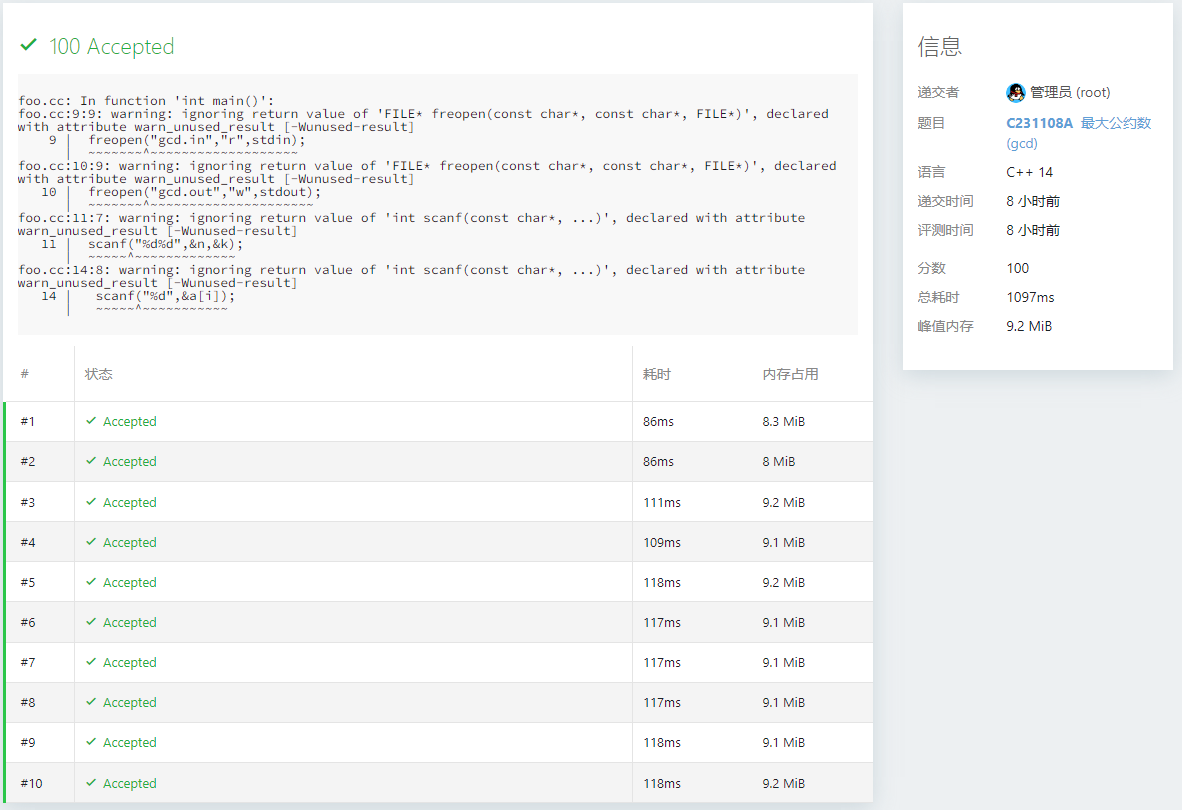
代码:
$\qquad$这个是 superl61 的代码,按照我的方法打的。
$\qquad$博客网址: superl61
#include<cstdio>
#include<ctype.h>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<bitset>
#define F(i,l,r) for(register int i=l;i<=r;++i)
#define G(i,r,l) for(register int i=r;i>=l;--i)
using std::min;
using std::max;
char buf[30],*p1=buf,*p2=buf;
inline int gc(){ return (p1==p2)&&(p2=(p1=buf)+fread(buf,1,30,stdin),p1==p2)?EOF:*p1++; }
inline int rd(){
int x=0; char ch=gc();
while(!isdigit(ch)) ch=gc();
while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=gc();
return x;
}
const int M=1e6+5;
int n,k,x,mi[M],ma[M];
std::bitset<M> b;
int main(){
freopen("gcd.in","r",stdin);
freopen("gcd.out","w",stdout);
n=rd(),k=rd(),memset(mi,0x3f,sizeof(mi));
F(i,1,n) {
x=rd();
mi[x]=min(mi[x],i);
ma[x]=max(ma[x],i);
b[M-x]=1;
}
for(int i=b._Find_first();M-i<=M;i=b._Find_next(i)){
int p=M-i;
if(ma[p]-mi[p]>=k) return printf("%d\n",p),fflush(0),fclose(stdin),fclose(stdout),0;
int q=(int)sqrt(p);
F(j,2,q) if(!(p%j)){
b[M-j]=b[M-p/j]=1;
mi[j]=min(mi[j],mi[p]),ma[j]=max(ma[j],ma[p]);
mi[p/j]=min(mi[p/j],mi[p]),ma[p/j]=max(ma[p/j],ma[p]);
}
}
puts("1");
fflush(0),fclose(stdin),fclose(stdout);
return 0;
}


