#C231229A. 「NOI2007」社交网络

标签（Label）

最短路算法

前言（Front talk)

$\qquad$这是Floyd的进阶，我觉得非常的妙。

网址（Website）

$\qquad$题目详情 - 「NOI2007」社交网络 - Super

$\qquad$P2047 [NOI2007] 社交网络 - 洛谷

题目（Problem）

$\qquad$ 在社交网络 ( Social Network ) 的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题:

$\qquad$ 在一个社交圈子里有 $n$ 个人，人与人之间有不同程度的关系。我们将这个关系网络对应到一个 $n$ 个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值 $c$ ，$c$ 越小，表示两个人之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人 $s$ 和 $t$ 之间的关系密切程度，注意到最短路径上的其他结点为 $s$ 和 $t$ 的联系提供了某种便利，即这些结点对于 $s$ 和 $t$ 之间的联系有一定的重要程度。我们可以通过统计经过一个结点 $v$ 的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点 $A$ 和 $B$ 之间可能会有多条最短路径。我们修改重要程度的定义如下：令 $C_{s,t}$ 表示从s到t的不同的最短路的数目，$C_{s,t}(v)$ 表示经过 $v$ 从 $s$ 到 $t$ 的最短路的数目；则定义：

$\qquad\qquad\qquad\qquad\qquad\qquad I(v)=\sum_{s \ne v,t\ne v} \frac{C_{s,t}(v)}{C_{s,t}}$

$\qquad$为结点 $v$ 在社交网络中的重要程度。为了使 $I(v)$ 和 $C_{s,t}(v)$ 有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图，请你求出每一个结点的重要程度。

输入格式

$\qquad$输入第一行有两个整数 $n$ 和 $m$ ，表示社交网络中结点和无向边的数目。
在无向图中，我们将所有结点从 $1$ 到 $n$ 进行编号。

$\qquad$接下来 $m$ 行，每行用三个整数 $a , b , c$ 描述一条连接结点 $a$ 和 $b$ ，权值为 $c$ 的无向边。
注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

输出格式

$\qquad$输出包括 $n$ 行，每行一个实数，精确到小数点后 $3$ 位。第 $i$ 行的实数表示结点 $i$ 在社交网络中的重要程度。

样例 #1

样例输入 #1

样例输出 #1

提示

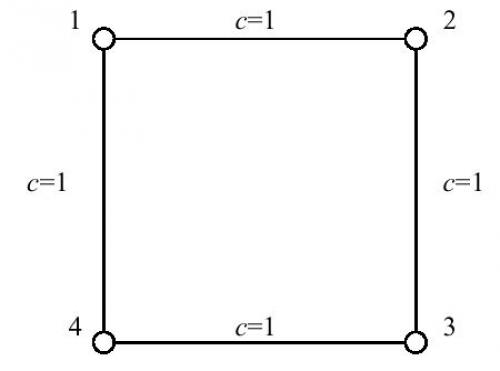
$\qquad$对于1号结点而言，只有2号到4号结点和4号到2号结点的最短路经过1号结点，而2号结点和4号结点之间的最短路又有2条。因而根据定义，1号结点的重要程度计算为1/2+1/2=1。由于图的对称性，其他三个结点的重要程度也都是1。

$\qquad$对于 $50%$ 的数据， $n \le 10 , m \le 45$。
$\qquad$对于 $100%$ 的数据， $n \le 100 , m \le 4500$ ，任意一条边的权值 $c$ 是正整数且 $1 \leqslant c \leqslant 1000$ 。所有数据中保证给出的无向图连通，且任意两个结点之间的最短路径数目不超过 $10^{10}$。

题解（Solution）

$\qquad$这道题非常的妙。

$\qquad$刚刚看到时，我一直在想这道题要怎么求出每个点是不是一条路径的最短路，然后就一直没有思路。

$\qquad$结果这道题用神奇的 $Floyd$ 算法做。

$\qquad$可知，令 $mp[x][y]$ 表示点 $x$ 到点 $y$ 的最短路，那么如果满足 $mp[x][y]=mp[x][k]+mp[k][y]$ ，则点 $k$ 一定在点 $x$ 与点 $y$ 的最短路上，那么，再思考如何求出最短路的条数。

$\qquad$设 $ed[x][y]$ 表示点 $x$ 到点 $y$ 的最短路径条数，我们通过每次判断最短路来计入路径，于是有：

For(k,1,n) For(i,1,n) For(j,1,n){//O(n^3)
	if(mp[i][k]==inf && mp[k][j]==inf) continue;
	if(mp[i][j]>mp[i][k]+mp[k][j]){
		ed[i][j]=ed[i][k]*ed[k][j];
		mp[i][j]=mp[i][k]+mp[j][k];
	}else if(mp[i][j]==mp[i][k]+mp[k][j]){
		ed[i][j]+=ed[i][k]*ed[k][j];
	}
}

$\qquad$那么可得当 $mp[x][y]=mp[x][k]+mp[k][y]$ 时，这个点的重要程度 $ansd[k]$ 会加上 $ed[i][k]\times ed[k][j]\div ed[i][j]$ ，有：

For(k,1,n) For(i,1,n) For(j,1,n){
	if(i==j || j==k || k==i) continue;
	if(mp[i][j]==mp[i][k]+mp[k][j]){
		ans[k]+=1.0*ed[i][k]*ed[k][j]/ed[i][j];
	} 
}

$\qquad$那么最终的答案就得出来了，这道题的经典之处在于 $mp[x][y]=mp[x][k]+mp[k][y]$ 这一个判断，其实可以通过 $n\le 100$ 这个条件看出要用 $Floyd$ 算法，但是我当时看到路径之后就只在想如何用 $dijkstra$ 或者 $spfa$ 来记录最短路径，然后发现越想脑壳越晕，这告诉我们做题之前要先想想这道题和哪些算法有关，才能保证走上正确的道路。

代码（Code）

#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int>
#define int long long
inline int input(){int x;return cin>>x,x;}
const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 105;
int mp[N][N],ed[N][N];
double ans[N];
int n,m;
signed main(){ 
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	memset(mp,0x3f,sizeof mp);
	cin>>n>>m;For(i,1,m){
		int x=input(),y=input(),v=input();
		mp[x][y]=mp[y][x]=v;
		ed[x][y]=ed[y][x]=1;
	}For(k,1,n) For(i,1,n) For(j,1,n){//O(n^3)
		if(mp[i][k]==inf && mp[k][j]==inf) continue;
		if(mp[i][j]>mp[i][k]+mp[k][j]){
			ed[i][j]=ed[i][k]*ed[k][j];
			mp[i][j]=mp[i][k]+mp[j][k];
		}else if(mp[i][j]==mp[i][k]+mp[k][j]){
			ed[i][j]+=ed[i][k]*ed[k][j];
		}
	}For(k,1,n) For(i,1,n) For(j,1,n){
		if(i==j || j==k || k==i) continue;
		if(mp[i][j]==mp[i][k]+mp[k][j]){
			ans[k]+=1.0*ed[i][k]*ed[k][j]/ed[i][j];
		} 
	}For(i,1,n) printf("%.3lf\n",ans[i]);
	return 0;
}