#C240812B.「NOIP2023」三值逻辑
标签(Label)
- 图论转化
- 深搜
前言(Front talk)
$\qquad$去年没有做出来主要是两个问题:1.考场上太急,没有认真分析就开始做;2.没有细心模拟样例。
$\qquad$这道题确实是转化为图论来做,但是由于没有分析好样例,导致我那时抓着半截就走,从一开始方向就错了。
网址(Website)
题目(Problem)
题目描述
小 L 今天学习了 Kleene 三值逻辑。
在三值逻辑中,一个变量的值可能为:真($\mathit{True}$,简写作 $\mathit{T}$)、假($\mathit{False}$,简写作 $\mathit{F}$)或未确定($\mathit{Unknown}$,简写作 $\mathit{U}$)。
在三值逻辑上也可以定义逻辑运算。由于小 L 学习进度很慢,只掌握了逻辑非运算 $\lnot$,其运算法则为:
$$\lnot \mathit{T} = \mathit{F}, \lnot \mathit{F} = \mathit{T}, \lnot\mathit{U} = \mathit{U}.$$
现在小 L 有 $n$ 个三值逻辑变量 $x_1,\cdots, x_n$。小 L 想进行一些有趣的尝试,于是他写下了 $m$ 条语句。语句有以下三种类型,其中 $\leftarrow$ 表示赋值:
- $x_i \leftarrow v$,其中 $v$ 为 $\mathit{T}, \mathit{F}, \mathit{U}$ 的一种;
- $x_i \leftarrow x_j$;
- $x_i \leftarrow \lnot x_j$。
一开始,小 L 会给这些变量赋初值,然后按顺序运行这 $m$ 条语句。
小 L 希望执行了所有语句后,所有变量的最终值与初值都相等。在此前提下,小 L 希望初值中 $\mathit{Unknown}$ 的变量尽可能少。
在本题中,你需要帮助小 L 找到 $\mathit{Unknown}$ 变量个数最少的赋初值方案,使得执行了所有语句后所有变量的最终值和初始值相等。小 L 保证,至少对于本题的所有测试用例,这样的赋初值方案都必然是存在的。
输入格式
本题的测试点包含有多组测试数据。
输入的第一行包含两个整数 $c$ 和 $t$,分别表示测试点编号和测试数据组数。对于样例,$c$ 表示该样例与测试点 $c$ 拥有相同的限制条件。
接下来,对于每组测试数据:
- 输入的第一行包含两个整数 $n$ 和 $m$,分别表示变量个数和语句条数。
- 接下来 $m$ 行,按运行顺序给出每条语句。
- 输入的第一个字符 $v$ 描述这条语句的类型。保证 $v$ 为
TFU+-的其中一种。 - 若 $v$ 为
TFU的某一种时,接下来给出一个整数 $i$,表示该语句为 $x_i \leftarrow v$; - 若 $v$ 为
+,接下来给出两个整数 $i,j$,表示该语句为 $x_i \leftarrow x_j$; - 若 $v$ 为
-,接下来给出两个整数 $i,j$,表示该语句为 $x_i \leftarrow \lnot x_j$。
- 输入的第一个字符 $v$ 描述这条语句的类型。保证 $v$ 为
输出格式
对于每组测试数据输出一行一个整数,表示所有符合条件的赋初值方案中,$\mathit{Unknown}$ 变量个数的最小值。
样例 #1
样例输入 #1
1 3
3 3
- 2 1
- 3 2
+ 1 3
3 3
- 2 1
- 3 2
- 1 3
2 2
T 2
U 2样例输出 #1
0
3
1提示
【样例解释 #1】
第一组测试数据中,$m$ 行语句依次为
- $x_2 \leftarrow \lnot x_1$;
- $x_3 \leftarrow \lnot x_2$;
- $x_1 \leftarrow x_3$。
一组合法的赋初值方案为 $x_1 = \mathit{T}, x_2 = \mathit{F}, x_3 = \mathit{T}$,共有 $0$ 个$\mathit{Unknown}$ 变量。因为不存在赋初值方案中有小于 $0$ 个$\mathit{Unknown}$ 变量,故输出为 $0$。
第二组测试数据中,$m$ 行语句依次为
- $x_2 \leftarrow \lnot x_1$;
- $x_3 \leftarrow \lnot x_2$;
- $x_1 \leftarrow \lnot x_3$。
唯一的赋初值方案为 $x_1 = x_2 = x_3 = \mathit{U}$,共有 $3$ 个$\mathit{Unknown}$ 变量,故输出为 $3$。
第三组测试数据中,$m$ 行语句依次为
- $x_2 \leftarrow \mathit{T}$;
- $x_2 \leftarrow \mathit{U}$;
一个最小化 $\mathit{Unknown}$ 变量个数的赋初值方案为 $x_1 = \mathit{T}, x_2 = \mathit{U}$。$x_1 = x_2 = \mathit{U}$ 也是一个合法的方案,但它没有最小化 $\mathit{Unknown}$ 变量的个数。
【样例解释 #2】
该组样例满足测试点 $2$ 的条件。
【样例解释 #3】
该组样例满足测试点 $5$ 的条件。
【样例解释 #4】
该组样例满足测试点 $8$ 的条件。
【数据范围】
对于所有测试数据,保证:
- $1 \le t \le 6$,$1 \le n,m \le 10 ^ 5$;
- 对于每个操作,$v$ 为
TFU+-中的某个字符,$1 \le i,j \le n$。
| 测试点编号 | $n,m\leq$ | $v$ 可能的取值 |
|---|---|---|
| $1,2$ | $10$ | $\mathit{TFU+-}$ |
| $3$ | $10^3$ | $\mathit{TFU}$ |
| $4$ | $10^5$ | $\mathit{TFU}$ |
| $5$ | $10^3$ | $\mathit{U+}$ |
| $6$ | $10^5$ | $\mathit{U+}$ |
| $7$ | $10^3$ | $\mathit{+-}$ |
| $8$ | $10^5$ | $\mathit{+-}$ |
| $9$ | $10^3$ | $\mathit{TFU+-}$ |
| $10$ | $10^5$ | $\mathit{TFU+-}$ |
题解(Solution)
$\qquad$分析样例以及数据范围,可以发现每个值最终的结果只和最后一次操作有关,这个地方很容易误导我们直接倒着做,但是中间被覆盖的操作虽然对当前位置没有影响,却会影响到其他的位置,因此,到这座反而更加的麻烦。
$\qquad$考虑正向分析,这里用了样例二中的第二组数据:
1 1
10 10
- 7 6
+ 4 1
+ 6 4
T 1
+ 2 9
- 9 10
U 10
+ 5 5
U 8
T 3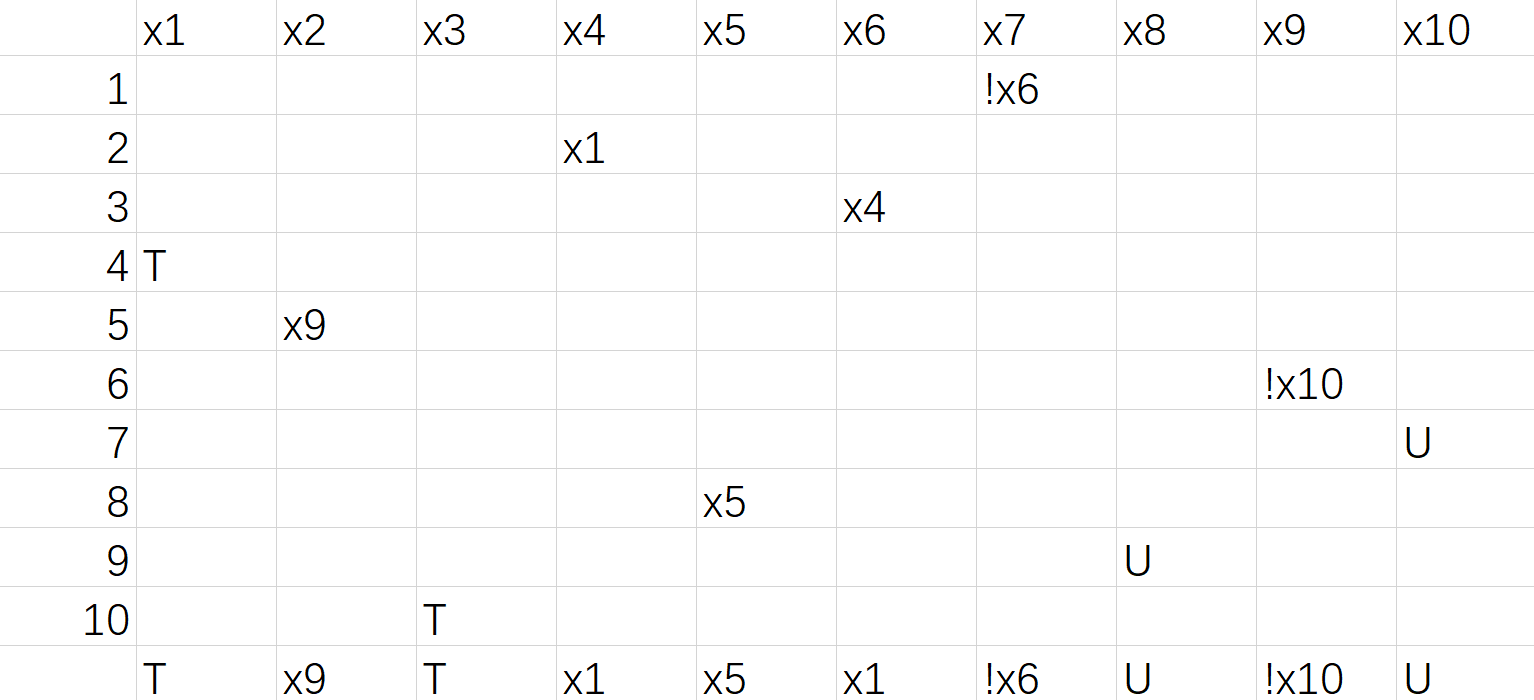
$\qquad$注意图中的 $x_6$ 位置,由于其被赋值为 $x_4$ ,而此时的 $x_4$ 的值为 $x1$ ,因此我们可以直接将其赋值为 $x_1$ 。可见,最终每个 $x_i$ 值只有 $5$ 中情况:$T$、$F$、$U$、$x_j$、$!x_j$ 。
$\qquad$发现位置之间的关系可以转化为图上点与点之间的关系,于是我们考虑依照最后的关系建无向图,建出来的图最终会是几个连通块的形式。对于每个连通块,如果里面存在 $T$ 、$F$ 中的任意一个,那么这个图中的所有点都一定是 $T$ 、$F$;如果存在 $U$ ,那么所有的点都是 $U$ ;如果都没有,那么我们可以尝试令其中任意一个点为 $T$ ,若最终没有矛盾,那么这个连通块里面的所有点都可以成为$T$或$F$,否则只能全部为 $U$ 。因为题目保证一定有解,出现$T$ 、$F$的联通块中一定不会有$U$,且出现$U$的联通块中一定不会有$T$ 、$F$。
$\qquad$时间复杂度:$O(n+m)$
$\qquad$后补:对于如何建边,以下标为 $x,y$ ,是否取反为边权 $v$ ,搜索时只需要看边权 $v$ ,就知道 $x$ 、$y$ 两点是相同还是相反了。
代码(Code)
#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int>
#define int long long
#define fi first
#define se second
inline int rd(){int x;return cin>>x,x;}
const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2012345;
vector<P> ft[N];
int n,m,ans,a[N];
#define T (n+1)
#define F (n+2)
#define U (n+3)
inline int f(int x){
if(x==T) return F;else
if(x==F) return T;else
if(x==U) return U;
else return -x;
}
bitset<N> vst;
int siz[N];
inline void dfs_col(int x){
siz[x] = vst[x] = true;
for(auto p:ft[x]){
int y = p.fi, v = p.se;
if(a[y]) assert(v?a[x]==a[y]:a[x]==f(a[y]));
else{
a[y] = v ? a[x] : f(a[x]);
dfs_col(y);
siz[x] += siz[y];
}
}
}
inline bool dfs_nxt(int x){
siz[x] = vst[x] = true;
bool flg = false;
for(auto p:ft[x]){
int y = p.fi, v = p.se;
if(a[y]){
int chk = v ? a[x] : f(a[x]);
if(chk!=a[y]) flg = true;
}else{
a[y] = v ? a[x] : f(a[x]);
flg |= dfs_nxt(y);
siz[x] += siz[y];
}
}return flg;
}
//多测清空
signed main(){
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int Tim = clock(), tid=rd(), TT=rd();
cerr<<"TID:"<<tid<<'\n';
while(TT--){
cin>>n>>m;
fill(siz,siz+n+1,0);vst.reset();
fill(a,a+n+1,0);ans = 0;
For(i,1,n) ft[i].clear();
while(m--){
char v;cin>>v;
if(v=='+'||v=='-'){
int i,j;cin>>i>>j;
if(a[j]) a[i] = v=='+' ? a[j] : f(a[j]);
else a[i] = v=='+' ? j : -j;
}else{
int i = rd();
switch(v){
case 'T':{a[i] = T;break;}
case 'F':{a[i] = F;break;}
case 'U':{a[i] = U;break;}
}
}
}For(i,1,n) cerr<<a[i]<<' ';cerr<<'\n';
//以点建边
For(i,1,n){
int x = i, y = abs(a[i]);
if(1<=y && y<=n){
if(a[i]>0){
ft[x].emplace_back(y,1);
ft[y].emplace_back(x,1);
}else
if(a[i]<0){
ft[x].emplace_back(y,0);
ft[y].emplace_back(x,0);
}a[i] = 0;//将颜色调为 0
}
}
For(x,1,n) if(a[x]>n && !vst[x]) dfs_col(x), ans += a[x]==U?siz[x]:0;
For(x,1,n) if(a[x]<=n){
a[x]=T;
if(dfs_nxt(x))
ans += siz[x];
}
cout<<ans<<'\n';
}return cerr<<"TIME:"<<(clock()-Tim)/1000.,0;
}


