#C240813B. mask

标签（Label）

• 扫描线
• 逆向思维

网址（Website）

题目详情 - mask - Super

题解 - mask - Super

题解（Solution）

发现正向计算比较麻烦，考虑逆向进行。易计算得如果没有任何一条斜边最终的答案是 $ans=(q+1)\times \frac{p\times (p+1)}{2}+(p+1)\times \frac{q\times (q+1)}{2}$ 。

如果加入一条斜边，这条斜边会使自己影响到的所有的点最终计算的距离 $-1$ ，而这个斜边能影响到的点就是它后面的一个矩形区域，易计算得对于从 $(x,y)$ 走到 $(x+1,y+1)$ 得斜边，其对答案的贡献是 $(p-x)\times (q-y)$

令 $f[i]$ 表示走到斜边 $(x_i,y_i)$ 前最多能走多少条斜边，则所有 $f[i]$ 相等的斜边最终影响到的点会组成如图得形状：

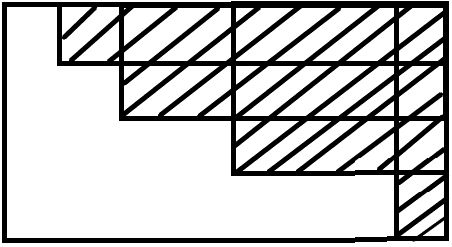
考虑如何求得 $f[i]$ ，发现 $f[i]$ 的求法与一道树状数组经典题很相像，我考试的时候还不知道这个思路叫扫描线，直接用树状数组维护，实时更新，将每次计算得到的 $f[i]$ 用 vector 存下来（最多有 $n$ 条斜边，因此 $f[i]$ 最大为 $n$ ），最后计算上图所示的面积之和即为总共减少的距离，用 $ans$ 减去即可。

代码（Code）

#include<bits/stdc++.h>
#include<vector>
#include<queue>
#include<map>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){int x;return cin>>x,x;}
const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 2012345;
const int C = 5;

int n,p,q,ans;
struct node{int x,y,v;}a[N];

#define lbt(x) (x&-x)
int c[N];
inline void update(int x,int v){for(int i=x;i<=p+C;i+=lbt(i))c[i]=max(c[i],v);}
inline int ask(int x){assert(x>=0);int res=0;for(int i=x;i;i-=lbt(i))res=max(c[i],res);return res;}

vector<P> pos[N];

signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	freopen("mask.in","r",stdin),
	freopen("mask.out","w",stdout);
	cin>>n>>p>>q;int Tim = clock();
	
	ans = (q+1)*p*(p+1)/2+q*(p+1)*(q+1)/2;
	
	For(i,1,n){
		int x,y;cin>>x>>y;
		a[i] = {x,y};
	}
	sort(a+1,a+n+1,[&](node a,node b){return a.y==b.y?a.x>b.x:a.y<b.y;});
	For(i,1,n){
		int vl = ask(a[i].x-1+C)+1;
		pos[vl].emplace_back(a[i].x,a[i].y);
		update(a[i].x+C,vl);
	}
	For(i,0,n){
		int lst = q, sum = 0;
		sort(pos[i].begin(),pos[i].end(),[&](P a,P b){return a.x==b.x?a.y>b.y:a.x<b.x;});
		for(auto pr:pos[i]){
			int x = pr.x, y = pr.y;
			sum += (lst-y)*(p-x);
			lst = y;
		}ans -= sum;
	}cout<<(ans)<<'\n';
	return cerr<<"TIME:"<<(clock()-Tim)/1000.,0;
}