#C241101B. 删除

标签（Label）

动态规划
思维

网址（Website）

题目详情 - 删除 - Super

题解 - 删除 - Super

改编自： D - Erase Balls 2D (atcoder.jp)

题目（Problem）

样例说明及数据

输入数据 1

输出数据 1

【样例1解释】

可能的集合有 ${1, 2, 3}, {1, 2}, {1, 3}$。

输入数据 2

输出数据 2

【样例2解释】

可能的集合有 ${1, 2, 3, 4}, {1, 3, 4}, {2, 4}$。

【样例3】

见选手目录下的 $\text{del/del3.in}$ 与 $\text{del/del3.ans}$。

【样例4】

见选手目录下的 $\text{del/del4.in}$ 与 $\text{del/del4.ans}$。

【样例5】

见选手目录下的 $\text{del/del5.in}$ 与 $\text{del/del5.ans}$。

【样例6】

见选手目录下的 $\text{del/del6.in}$ 与 $\text{del/del6.ans}$。

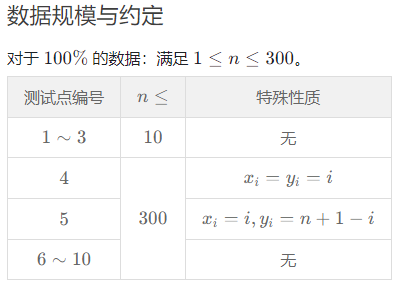
题解（Solution）

出题者题解

算法分析

改编自 ARC184D，这一点在题目背景里面已经提到了（。

考虑直接计数集合不太合适，所以考虑给每个剩余集合的方案都对应一种操作的方案。

我们考虑如下映射：

对于一个剩余的集合，如果一个点左下角没有点了，那么就钦定它操作一次 $1$，如果它右上角没有点了，那么就钦定它操作一次 $2$，注意，一个点可以都操作。

容易发现这一定是双射。

因为对于一个剩余的集合，它只能构造出一种这样的方案，而且，如果它是合法的，那么通过这个方法一定可以构造出来，因为你已经把所有能操作的部分全部操作了，如果还没有达成这个集合，那么目前的点一定无法被删掉。

而对于一个方案，我们只需要照着这个方案操作，就一定能得到唯一一个点集。

考虑这个方案的性质，可以发现，所有操作了左下角的点，一定排成一个 $x$ 递增，$y$ 递减的序列，并且，按照 $y$ 坐标的顺序从小到大排列的话，相邻两个点围成的矩形中间一定是没有任何别的点的。

这是因为这中间如果出现了其他点，那么一定可以从这些点（指中间的其他点）中选出一个左下角不存在别的点的点，那么这个点是可以进行 $1$ 操作的，所以这样就一定不是一个合法的操作方案。

对于操作了右上的点同理。

所以把所有点按照 $y$ 坐标从小到大排序，考虑设 $f_{i,j,k}$ 表示当前扫到了 $y=i$ 这一行，最近的一个 $1$ 操作在第 $j$ 个点上，最近的一个 $2$ 操作在第 $k$ 个点上，的方案数。

从 $i \rightarrow i+1$ 的转移可以直接分类：

若 $i+1$ 号点被包含在了 $1$ 操作或 $2$ 操作覆盖的部分，那么就无法操作，直接转移到 $f_{i+1,j,k}$。
若 $i+1$ 号点在 $j$ 号点的左上角，且中间没有别的点，那么就可以转移到 $f_{i+1,i+1,k}$。
若 $i+1$ 号点在 $k$ 号点的左上角，且中间没有别的点，那么就可以转移到 $f_{i+1,j,i+1}$。
若同时满足 $2,3$ 的两个条件，那么就可以转移到 $f_{i+1,i+1,i+1}$。
最后一定可以转移到 $f_{i+1,j,k}$，注意如果满足了 $1$ 的条件，那么就不进行这个转移。

为了方便实现，可以加入两个新的点 $(n+1,0)$ 和 $(0,n+1)$，$(n+1,0)$ 作为 $0$ 号点，而 $(0,n+1)$ 作为 $n+1$ 号点。

初始化为 $f_{0,0,0}=1$，答案即为 $f_{n+1,n+1,n+1}$。

出题人的实现：https://www.luogu.com.cn/paste/6kua1puv

代码（Code）

#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
#define inn(x,l,r) (l<=x && x<=r)
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}const int inf = 0x3f3f3f3f3f3f3f3f;
const int mod = 998244353;
const int N = 305;
bool ST;
inline void add(int &x,int y){if((x+=y)>=mod)x-=mod;}
inline void sub(int &x,int y){if((x-=y)<0)x+=mod;} 

int n,t[N];
P a[N];

struct Baoli{
	unordered_map<bitset<15>,bool> mp;
	bitset<15> del;int b[15];
	void kill(){
		For(i,1,n){
			if((b[i]==1||b[i]==3) && !del[i]){For(j,1,n) if(a[j].x<a[i].x && a[j].y<a[i].y) del[j] = true;}
			if((b[i]==2||b[i]==3) && !del[i]){For(j,1,n) if(a[j].x>a[i].x && a[j].y>a[i].y) del[j] = true;}
		}mp[del]=true, del.reset();
		Rof(i,n,1){
			if((b[i]==1||b[i]==3) && !del[i]){For(j,1,n) if(a[j].x<a[i].x && a[j].y<a[i].y) del[j] = true;}
			if((b[i]==2||b[i]==3) && !del[i]){For(j,1,n) if(a[j].x>a[i].x && a[j].y>a[i].y) del[j] = true;}
		}mp[del]=true, del.reset();
	}
	void dfs(int i){
		if(i==n+1) return kill();
		for(int j:{0,1,2,3}){
			b[i] = j, dfs(i+1);
		}
	}
	inline bool check0(){return n<=10;}
	inline bool check1(){bool flag = true;For(i,1,n) flag &= a[i].x==i&&a[i].y==n-i+1;return flag;}
	inline bool check2(){bool flag = true;For(i,1,n) flag &= a[i].x==i&&a[i].y==i;return flag;}
	void Solve0(){dfs(1),printf("%lld\n",mp.size());}
	void Solve1(){printf("1\n");}
	void Solve2(){printf("%lld\n",n*(n+1)/2);}
}Q;

bitset<N> can[N];//判断两个点之间有没有值 
int f[N][N][N];

void Solve(){
	n=rd();For(i,1,n) a[i]={rd(),rd()}, t[a[i].y] = a[i].x;
	if(Q.check0()) return Q.Solve0();
	if(Q.check1()) return Q.Solve1();
	if(Q.check2()) return Q.Solve2();
	
	For(i,0,n+1) can[i] = ~can[i];
	t[0]=n+1, t[n+1]=0;
	
	For(i,1,n+1) For(j,0,i-1) For(k,0,j-1){//这里枚举的是高度 
		if(inn(t[j], t[i], t[k])) can[i][k] = can[k][i] = false;
	}
	
	f[0][0][0] = 1;
	For(i,0,n) For(j,0,i) For(k,0,i){
		add(f[i+1][j][k], f[i][j][k]);//这个点被覆盖/这个点本来就什么都不能干
		if(t[i+1]>t[k]) continue;
		bool chk1 = (t[i+1]<t[j] && can[i+1][j]);
		bool chk2 = (t[i+1]<t[k] && can[i+1][k]);
		if(chk1) add(f[i+1][i+1][k], f[i][j][k]);
		if(chk2) add(f[i+1][j][i+1], f[i][j][k]);
		if(chk1&&chk2) add(f[i+1][i+1][i+1], f[i][j][k]);
	}
	printf("%lld\n", f[n+1][n+1][n+1]);
} 

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("del.in","r",stdin);
	freopen("del.out","w",stdout);
	int T=1;double Tim=clock();
	while(T--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}