#C241112A. 石子游戏
标签(Label)
- 数学
- 博弈论
网址(Website)
题目(Problem)

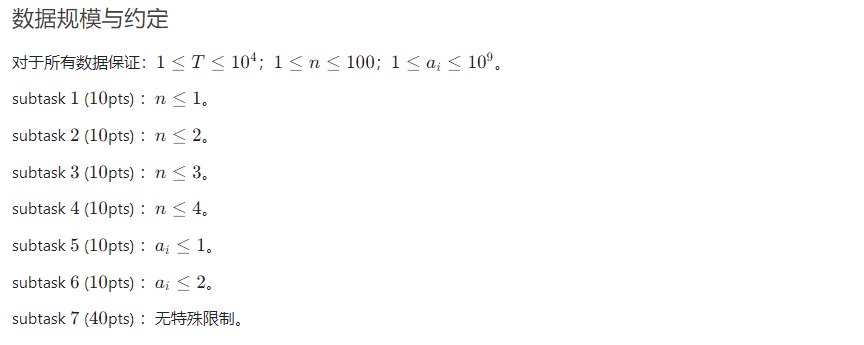
题解(Solution)
$\qquad$我c,我原来竟然想对了?但是好像代码写挂了。。。
$\qquad$。。。好吧,想挂了。
$\qquad$这道题对于分类讨论的能力考验非常好!!!
$\qquad$发现 $1$ 非常的特殊,直接开始枚举 $1$ 。容易枚举到一堆 1 和一个 $x$ 的情况。
出题者题解
算法分析
全 1 的话先手赢当且仅当 $n \mod 3 \neq 0$。
如果是一堆 1 和一个 $x$,先手可以选择把 $x$ 取干净,剩余 $n - 1$ 个 1,或把 $x$ 取到 1,剩余 $n$ 个 1。两种可能至少有一个会赢,因此一堆 1 和一个 $x$ 先手必胜。
假设初始有 $k (k > 1)$ 个数大于 1,后手需要尽量控制 $k \neq 1$。
若后手操作之前 $k = 2$,则后手有三种选择:把两个大于 1 的堆取到 1,把一个取到 1 另一个取干净,两个都取干净。三种选择恰好有一种获胜,因此后说操作前如果 $k = 2$,则后手必胜。
若后手操作之前 $k = 1$ 且唯一比 1 大的元素大于 2,则后手有三种选择:把一堆大于 1 的取到 1,把一堆大于 1 的取到 0,把两堆取到 0。三种选择恰好一种获胜,因此此时后手必胜。
当初始情况 $k = 2$ 时,先手想赢必须初始石子是一堆 $1$ 一个 $2$ 一个 $x$ 且 $n \mod 3 \neq 2$,先手把 $x$ 取干净或把 $x$ 取成 $1$。当初始情况 $k > 2$ 时,后手可以把 $n\ \text{mod}$ 调整对。先手无法避免 $k = 2$ 的情况,此时 $n \mod 3$ 不对,于是剩余情况后手必胜。
代码(Code)
#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){
char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 105;
bool ST;
int n,a[N];;
void Solve(){
n=rd();For(i,1,n) a[i]=rd();
sort(a+1,a+n+1);
if(n%3==0 && a[n]==1) puts("Lose");else
if(n==1 || a[n-1]==1) puts("Win");else
if(n%3!=2 && a[n-2]==1 && a[n-1]==2) puts("Win");
else puts("Lose");
}
bool ED;
signed main(){
cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
freopen("stone.in","r",stdin);
freopen("stone.out","a",stdout);
int Tt=rd();double Tim=clock();
while(Tt--) Solve();
return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}


