#C241115B. B
标签(Label)
- 根号分治
- 数学
网址(Website)
题目(Problem)

样例
输入数据 1
2 4
1 2
3 4
5 6输出数据 1
10【样例1解释】
集合 $S = {9, 10, 10, 10, 11, 11, 11, 12}$,第 $4$ 小的值是 $10$ 。
输入数据 2
10 40
11 9 13 12 15 11 11 2 11 17
3 1 10 2 12 18 9 11 11 15
14 9 4 14 16 9 20 2 1 18输出数据 2
14【样例3】
见选手目录下的 set/set3.in 与 set/set3.ans。
【样例4】
见选手目录下的 set/set4.in 与 set/set4.ans。
【样例5】
见选手目录下的 set/set5.in 与 set/set5.ans。
【样例6】
见选手目录下的 set/set6.in 与 set/set6.ans。

题解(Solution)
这道题很卡常,不要用结构体。
肯定先对每个数字排序,这个不必说。
33分
这道题的答案满足单调性(即对于最后的答案,小于它的点排名一定小于 $k$ ,否则一定大于 $k$)。
有一个很简单的想法就是二分 $mid$ ,求出排名。可以暴力枚举 $a_{i}$ ,那么就是要求 $b_j+c_k\le mid-a_i$ 的数有多少个,这个时候就可以直接枚举 $j$ ,发现 $j$ 变大的过程中 $b_j$ 变大,此时 $c_k$ 只能变小,则 $k$ 的范围一定变小,那么可以双指针 $O(n)$ 解决这个问题。
时间复杂度 $O(n^2\log A)$ 。
52分
双指针必须是 $O(n)$ 的时间复杂度,不好优化。
只能考虑压缩数组来解决问题,发现第 $3$ 个点的 $k\le 10^5$ ,那就只需要计算出 $b_j$ 和 $c_k$ 能组成的前 $k$ 小的数字,然后再二分与 $a_i$ 暴力匹配,时间复杂度 $O(k\log A)$ 。
100分
提供两种做法:
人类智慧法
发现当 $k\le 10^9$ 时,我们枚举的 $b_j+c_k$ 其实没必要到 $10^9$ ,假设我们计算 $S=10^6$ 的数据(时间复杂度 $O(S\log S)$ ,肯定能过),我们得出前 $i$ 个 $a_i$ 最多可以拿到 $i\times S$ 的排名,假定答案在我们当前计算的 $a_i,b_j,c_k$ 内,那我们就能得出正确答案,而出题人出的数据是随机的。
实际可以自己造数据,看一下开多少时间和空间能过,大概率是对的。
ps:学校电脑里面的 Linux 本机跑 $2$ 秒,交到我们的超卡 $\text{OJ}$ 上面都才 $0.7$ 秒。。。简直无语 ̄へ ̄
正解
以如下方式画图,由于排序之后数组存在单调性,那么对于每个 $a_i$ ,能取到的点的范围大概是下图的形式,斜线左边的都是能取到的。

这启示我们找到一个分界点 $B$ ,前 $B$ 个 $a_i$ 直接使用 $33$ 分的双指针计算,后面的用 $52$ 分那个部分分只需要暴力计算出前 $cnt$ 个 $b_j+c_k$ ,这样就能算的最后的答案了。可以根据下图大致理解。
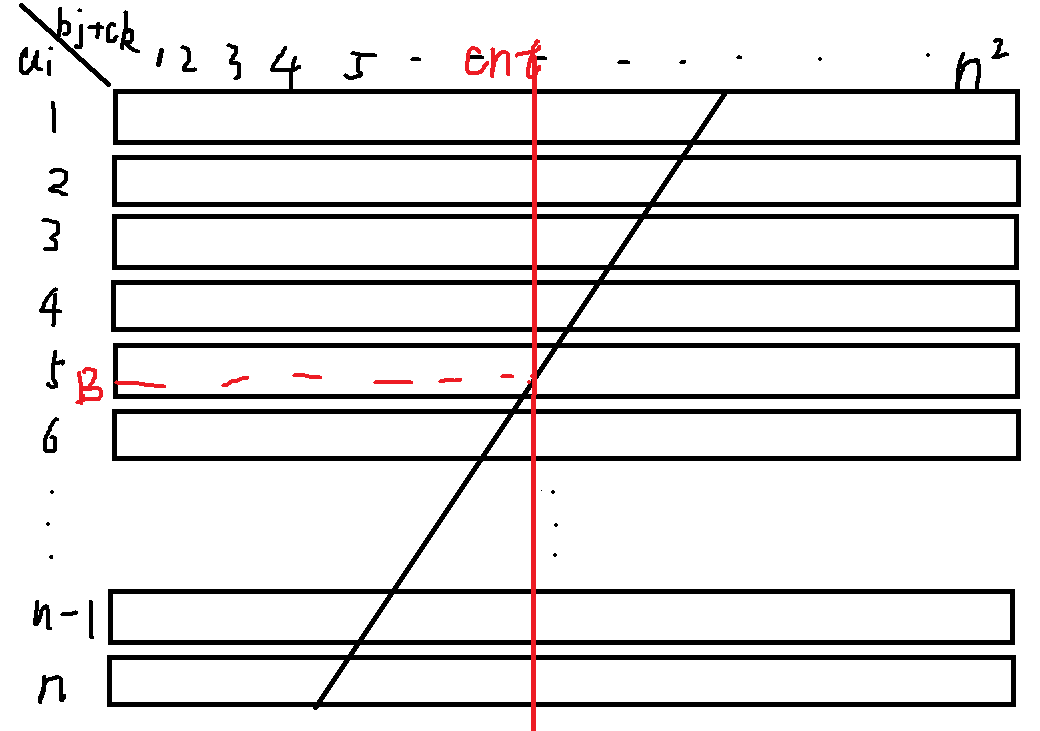
现在问题就是这个阈值 $B$ 该如何设定,前面的时间复杂度是 $O(nB\log A)$ 的,后面是 $O(cnt\times\log n+(n-B)\log cnt\log A)$ ,很明显 $cnt$ 的值远大于 $(n-B)$ ,那么只需要取 $O(cnt\times\log n)$ 的复杂度就好了,那么总复杂度为 $O(nB\log A+cnt\times\log n)$ 的,证明见题解。
出题者题解

代码(Code)
33分
#include<bits/stdc++.h> #include<vector> #define For(i,l,r) for(int i=l;i<=r;i++) #define Rof(i,l,r) for(int i=l;i>=r;i--) using namespace std; #define P pair<int,int> #define int long long #define x first #define y second inline int rd(){ bool f=false;char c;while(!isdigit(c=getchar()))f=c=='-';int x=c^48; while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x; }const int inf = 0x3f3f3f3f3f3f3f3f; const int N = 201234; const int S = 1e8; bool ST; int a[N],b[N],c[N]; int n,K,ans; inline bool chk(int mid){ int res = 0; for(int i=1;i<=n && a[i]<=mid;i++){ for(int j=1,k=n;j<=n && a[i]+b[j]<=mid;j++){ while(k && c[k] > mid-a[i]-b[j]) k--; res += k; } }return res >= K; } void Solve(){ n=rd(), K=rd();For(i,1,n) a[i]=rd();For(i,1,n) b[i]=rd();For(i,1,n) c[i]=rd(); sort(a+1,a+n+1), sort(b+1,b+n+1), sort(c+1,c+n+1); a[n+1] = b[n+1] = c[n+1] = inf; int l=0,r=3e9,mid; while(l<=r){ mid = (l+r)>>1; if(chk(mid)) ans=mid,r=mid-1; else l=mid+1; }printf("%lld\n", ans); } bool ED; signed main(){ cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n"; freopen("set.in","r",stdin); freopen("set.out","w",stdout); int Tt=1;double Tim=clock(); while(Tt--) Solve(); return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0; }
100分(人类智慧)
#include<bits/stdc++.h> #define For(i,l,r) for(int i=l;i<=r;i++) #define Rof(i,l,r) for(int i=l;i>=r;i--) using namespace std; #define P pair<int,int> #define int long long #define x first #define y second #define in(x,l,r) (l<=x && x<=r) inline int rd(){ char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48; while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x; }template<typename G> void write(G x){ if(x<0) putchar('-'),write(-x); else if(x<=9) putchar(x+'0'); else write(x/10), putchar(x%10+'0'); }constexpr int inf = 0x3f3f3f3f3f3f3f3f; constexpr int N = 201234; constexpr int S = 2000000; bool ST; int a[N],b[N],c[N],d[S+5]; int n,k,cnt; priority_queue<P> q; int calc(int mid){ int res = 0; for(int i=1,j=cnt;i<=n && a[i]<=mid;i++){ while(j && a[i]+d[j]>mid) j--; res += j; }return res; } void Solve(){ n=rd(),k=rd();For(i,1,n) a[i]=rd();For(i,1,n) b[i]=rd();For(i,1,n) c[i]=rd(); sort(a+1,a+n+1), sort(b+1,b+n+1), sort(c+1,c+n+1); For(i,1,n) q.emplace(-b[i]-c[1],1); while(q.size() && cnt<=S){ d[++cnt] = -q.top().x; int p = q.top().y;q.pop(); if(p<n) q.emplace(-d[cnt]+c[p]-c[p+1], p+1); } int l=a[1]+b[1]+c[1],r=a[n]+b[n]+c[n],res=-1; while(l<=r){ int mid = (l+r)>>1; if(calc(mid) >= k) r=mid-1,res=mid; else l=mid+1; }write(res), putchar('\n'); } bool ED; signed main(){ cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n"; freopen("set.in","r",stdin); freopen("set.out","w",stdout); int T = 1;double Tim = clock(); while(T--) Solve(); return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0; }
100分
#include<bits/stdc++.h> #include<vector> #include<queue> #define For(i,l,r) for(int i=l;i<=r;i++) #define Rof(i,l,r) for(int i=l;i>=r;i--) using namespace std; #define P pair<int,int> #define int long long #define x first #define y second inline int rd(){ char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48; while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x; }const int inf = 0x3f3f3f3f3f3f3f3f; const int N = 50123; const int M = 20123456; bool ST; int a[N],b[N],c[N]; int n,m,B,S,ans; priority_queue<pair<int,P>> q; int g[M],cnt; inline bool check(int mid){ int res = 0; For(i,1,B) for(int j=1,k=n;j<=n;j++){ while(k && b[j]+c[k] > mid-a[i]) k--; res += k; if(res >= m) return true; } For(i,B+1,n){ res += upper_bound(g+1,g+cnt+1,mid-a[i])-g-1; if(res >= m) return true; }return false; } void Solve(){ n=rd(), m=rd(), B=min((int)(sqrt(double(m)/n+1)),n), S=(m+B-1)/B; For(i,1,n) a[i]=rd();For(i,1,n) b[i]=rd();For(i,1,n) c[i]=rd(); sort(a+1,a+n+1), sort(b+1,b+n+1), sort(c+1,c+n+1); For(i,1,n) q.push({-b[i]-c[1],{i,1}}); while(q.size() && cnt<S){ P x=q.top().y;q.pop(); g[++cnt] = b[x.x]+c[x.y]; if(x.y<n) q.push({-b[x.x]-c[x.y+1],{x.x,x.y+1}}); } int l=a[1]+b[1]+c[1], r=a[n]+b[n]+c[n], mid; while(l<=r){ mid = (l+r)>>1; if(check(mid)) r=mid-1, ans=mid; else l=mid+1; }printf("%lld\n",ans); } bool ED; signed main(){ cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n"; freopen("set.in","r",stdin); freopen("set.out","w",stdout); int Tt=1;double Tim=clock(); while(Tt--) Solve(); return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0; }



