#C241119C. 多重集

标签（Label）

• 推式子
• 分类讨论

网址（Website）

题目详情 - 多重集 - Super

题解 - 多重集 - Super

题目（Problem）

输入数据 1

6
1 0 5 10
1 1 100 23
1 1 1 45
1 1 22 33
1 0 2 3
0 1 22 33

输出数据 1

-1
105
55
43
36
48

输入数据 2

4
1 1 1000000000 1
1 0 2 1000000000
1 0 500 12345678
0 1 1000000000 1

输出数据 2

-1
1000000002
1000000002
-1

【样例 3】

见附加文件中的 set/ex_set3.in 与 set/ex_set3.ans。

【样例 4】

见附加文件中的 set/ex_set4.in 与 set/ex_set4.ans。

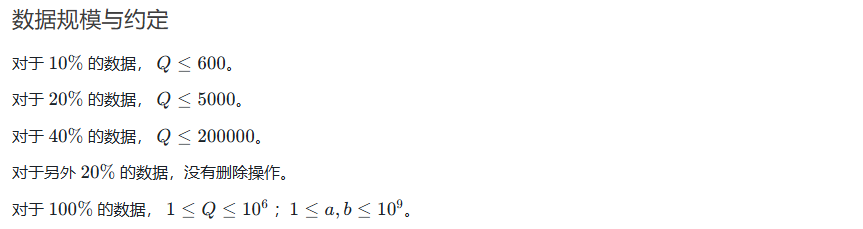
题解（Solution）

这里令 $n$ 表示询问（即题目中的 $Q$ ）。

20分

把每个元素存到数组里面（代码里面用的 $\verb!multiset!$ ，但是不影响总体复杂度），每次直接暴力匹配得到答案。

30分

用 $\verb!multiset!$ 处理，每新加入一个数就遍历另一个集合的 $\verb!multiset!$ 暴力维护答案，再将这些答案存到答案的 $\verb!multiset!$ 里面，单次 $O(n\log n)$ 。总时间复杂度 $O(n^2\log n)$ 。

100分

这道题的变量命名更 shit 一样。我们把两个多重集的每一对元素分别命名为 $A_x,A_y$ 和 $B_x,B_y$ 。

考虑推式子，把 $\max(A_x+B_x,A_y+B_y)$ 拆开，分类讨论：当 $A_x+B_x\ge A_y + B_y$ 的时候，有 $A_x-A_y\ge B_y-B_x$ ；当 $A_x+B_x\le A_y + B_y$ 的时候，有 $A_x-A_y\le B_y-B_x$ 。发现这一下处理之后就把每一个元素分开了。

建立值域线段树，设 $A_x-A_y$ 为集合 $A$ 中元素的键值，$B_y-B_x$ 就是集合 $B$ 中元素的键值。那么对于集合 $A$ 中的数就存到 $A_x-A_y$ 的位置，集合 $B$ 就存到 $B_y-B_x$ 的位置，对于 $A_x-A_y$ 或 $B_y-B_x$ 的位置，我们对每个位置开两个 $\verb!multiset!$ 分别存入它们的 $x$ 和 $y$ 。对于叶子节点，由于 $A_x-A_y = B_y-B_x$ ，因此答案就是 $\min(A_x+B_x,A_y+B_y)$ ；对于一个区间，我们分别记录区间中 $A,B$ 集合里面最小的 $A_x,A_y$ 和 $B_x,B_y$ ，由于是值域线段树，所以左子树的键值一定小于右子树。找到左边的 $A$ 集合中的元素和右边 $B$ 集合的元素，左右儿子能产生的新的最小答案就是 $A_y+B_y$ ；找到左边 $B$ 集合中的元素和右边 $A$ 集合中的元素，左右儿子能产生的新的最小答案就是 $A_x+B_x$ 。

注意初始化 $\verb!multiset!$ 的时候可以直接在里面加入一个极大值，这样就可以防止访问的时候要特判集合是否为空。

出题者题解

代码（Code）

20分

#include<bits/stdc++.h> 
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
#define show(a,b) {For(i,1,n) cerr<<a[i]<<b;cerr<<'\n';}
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
#define in(x,l,r) (l<=x && x<=r)
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1012345;
bool ST;double Tim;

multiset<P> s[2];

void Solve(){
	int q=rd();while(q--){
		int op=rd(),d=rd(),x=rd(),y=rd();
		if(op)	s[d].emplace(x,y);
		else 	s[d].erase({x,y});
		if(s[0].empty() || s[1].empty()){write(-1),puts("");continue;}
		int res = inf;
		for(auto a:s[0]) for(auto b:s[1]){
			res = min(res, max(a.x+b.x, a.y+b.y));
		}write(res),puts("");
	}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("set.in","r",stdin);
	freopen("set.out","w",stdout);
	int Tt=1;Tim=clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}

30分

#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1012345;
bool ST;double Tim;

multiset<P> s[2];
multiset<int> as;

void Solve(){
	int q=rd();while(q--){
		int op=rd(),d=rd(),x=rd(),y=rd();
		if(op){
			for(auto p:s[d^1]) as.emplace(max(x+p.x,y+p.y));
			s[d].emplace(x,y);
		}else{
			s[d].erase({x,y});
			for(auto p:s[d^1]) as.erase(as.find(max(x+p.x,y+p.y)));
		}
		if(as.empty()) write(-1), puts("");
		else write(*as.begin()), puts("");
	}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("set.in","r",stdin);
	freopen("set.out","w",stdout);
	int Tt=1;Tim=clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}

100分

#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
#define show(a,b) {For(i,1,n) cerr<<s[i]<<b;cerr<<'\n';}
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
#define in(x,l,r) (l<=x && x<=r)
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}const int inf = 0x3f3f3f3f3f3f3f3f;
const int N = 1012345;
bool ST;double Tim;

#define A 0
#define B 1

namespace tree{
	#define mid ((l+r)>>1)
	#define ls (p<<1)
	#define rs (p<<1|1)
	struct Tr{P mn[2];int ans;}tr[N<<2|3];
	multiset<int> s[N][2][2];//set也要初始化
	void build(int p,int l,int r){
		For(d,0,1) tr[p].mn[d] = {inf,inf}, tr[p].ans = inf;
		if(l==r){For(i,0,1) For(j,0,1) s[l][i][j].emplace(inf);return;}
		build(ls,l,mid), build(rs,mid+1,r);
	}
	inline void pushup(Tr &T,Tr L,Tr R){
		T.ans = min({L.ans, R.ans, L.mn[B].x+R.mn[A].x, L.mn[A].y+R.mn[B].y});
		For(d,0,1) T.mn[d] = {min(L.mn[d].x, R.mn[d].x), min(L.mn[d].y, R.mn[d].y)};
	}
	void modify(int opt,int p,int l,int r,int d,int pos,P val){
		if(l==r){
			if(opt==0){
				s[l][d][0].erase(s[l][d][0].find(val.x)), 
				s[l][d][1].erase(s[l][d][1].find(val.y));
			}else s[l][d][0].emplace(val.x), s[l][d][1].emplace(val.y);
			
			tr[p].mn[d] = {*s[l][d][0].begin(), *s[l][d][1].begin()}; 
			tr[p].ans = min(tr[p].mn[A].x+tr[p].mn[B].x, tr[p].mn[A].y+tr[p].mn[B].y);
			return;
		}
		if(pos<=mid) modify(opt,ls,l,mid,d,pos,val);
		else modify(opt,rs,mid+1,r,d,pos,val);
		pushup(tr[p],tr[ls],tr[rs]);
	}
}

int op[N],d[N],x[N],y[N];
int b[N],n,q;

void Solve(){
	q=rd();For(i,1,q){
		op[i]=rd(), d[i]=rd(), x[i]=rd(), y[i]=rd();
		if(op[i]) b[++n] = d[i] ? y[i]-x[i] : x[i]-y[i];
	}
	sort(b+1,b+n+1), n=unique(b+1,b+n+1)-b-1;
	tree::build(1,1,n);
	For(i,1,q){
		int tmp = d[i] ? y[i]-x[i] : x[i]-y[i];
		tmp = lower_bound(b+1,b+n+1,tmp)-b;
		tree::modify(op[i],1,1,n,d[i],tmp,{x[i],y[i]});
		tmp = tree::tr[1].ans;
		if(tmp==inf) tmp=-1;
		write(tmp), putchar('\n');
	}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("set.in","r",stdin);
	freopen("set.out","w",stdout);
	int Tt=1;Tim=clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}