#C241122A. 矩阵

标签（Label）

• 扩展域并查集
• 思维

网址（Website）

题目详情 - 矩阵 - Super

题解 - 矩阵 - Super

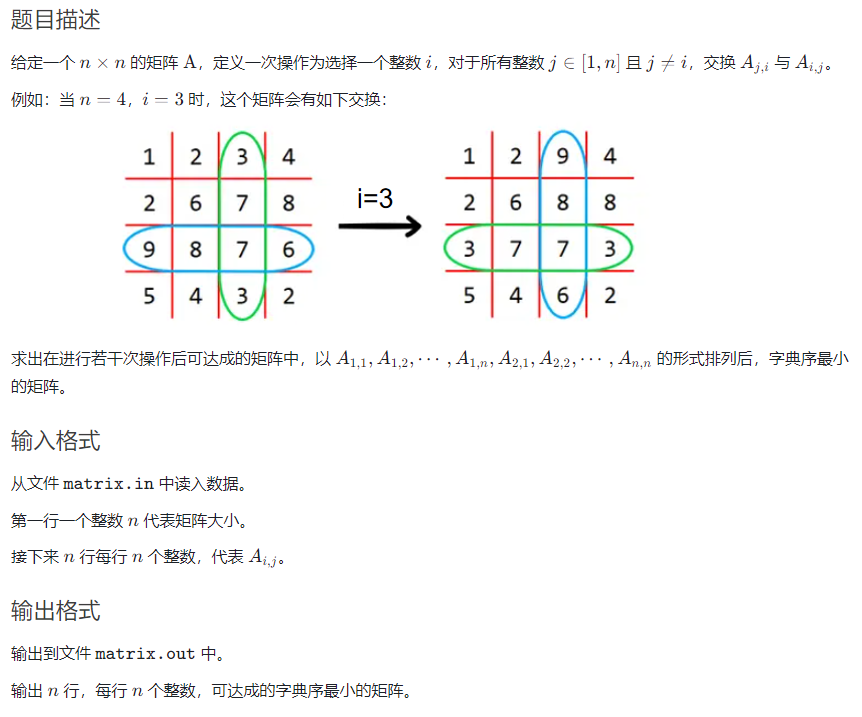
题目（Problem）

输入数据 1

3
2 1 2
2 1 2
1 1 2

输出数据 1

2 1 1
2 1 1
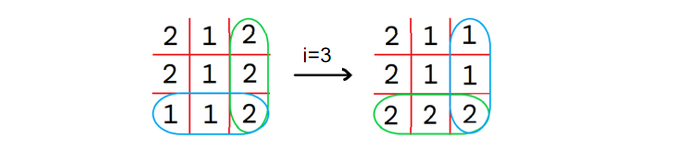
2 2 2

【样例1解释】

输入数据 2

4
3 3 1 2
1 1 3 1
3 2 3 2
2 3 3 1

输出数据 2

3 1 1 2
3 1 2 1
3 3 3 3
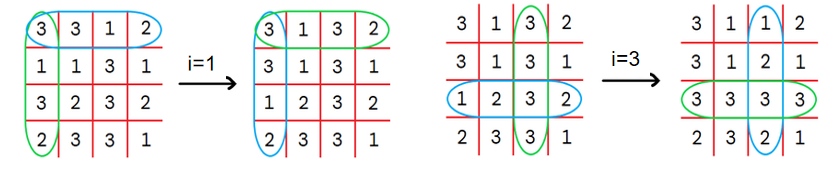
2 3 2 1

【样例2解释】

【样例3】

见选手目录下的 $matrix/matrix3.in$ 与 $matrix/matrix3.ans$。

【样例4】

见选手目录下的 $matrix/matrix4.in$ 与 $matrix/matrix4.ans$。

【样例5】

见选手目录下的 $matrix/matrix5.in$ 与 $matrix/matrix5.ans$。

题解（Solution）

95分（人类智慧法）

由于字典序自带前面一位更小就一定更小的性质，基本的贪心思路就是直接暴力模拟换 $a_{i,j}$ 。

容易发现 $a_{i,j}$ 只会和 $a_{j,i}$ 交换。

对于 $a_{i,j}$ ，分类讨论：

• 如果 $a_{i,j} < a_{j,i}$ ，不换就好了，这个时候我们要防止后面的数把这两个点交换，发现能影响到这两个点的行列只有对 $i$ 或者 $j$ 使用交换的操作，此时我们直接固定这两个点不能再被用来操作；
• 如果 $a_{i,j}=a_{j,i}$ ，随便换，没什么限制；
• 如果 $a_{i,j}>a_{j,i}$ ，肯定要交换，但是这个时候需要判断前面有没有已经固定的点，如果固定了肯定不能交换，否则就不优；如果发现可以交换，直接暴力交换，由于最多交换 $O(n)$ 次，每次交换是 $O(n)$ 的复杂度，所以总时间复杂度还是 $O(n^2)$ 的。

综上，时间复杂度 $O(n^2)$ ，只被卡了一个点，得分 $\text{95pts}$ 。

100分

发现前面的方法有一个地方伪掉了，如果有一个 $a_{i,j}$ ，我们发现 $a_{i,j}<a_{j,i}$ ，这个时候我们钦定 $i$ 和 $j$ 不能进行操作，但是我们其实可以对 $i$ 和 $j$ 都进行操作，这样并不会影响 $a_{i,j}<a_{j,i}$ ，然而都进行操作的答案可能更优。

再回顾一下每次交换的限制，分类讨论：

• 如果 $a_{i,j} < a_{j,i}$ ，要么操作 $2$ 次要么不操作，操作偶数次；
• 如果 $a_{i,j}=a_{j,i}$ ，随便换，没什么限制；
• 如果 $a_{i,j}>a_{j,i}$ ，在能操作的情况下，肯定要操作 $1$ 次最优。

这下就发现性质了，再往后想：

• 如果 $a_{i,j} < a_{j,i}$ ，对 $i$ 和 $j$ 交换的操作次数应相等；
• 如果 $a_{i,j}=a_{j,i}$ ，随便换，没什么限制；
• 如果 $a_{i,j}>a_{j,i}$ ，对 $i$ 和 $j$ 交换的操作次数应不同；

这个就是扩展域并查集的板子了，处理一下即可。

时间复杂度 $O(n^2)$ 。

出题者题解

代码（Code）

95分(人类智慧法)

#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define ROf(i,l,r) for(int i=l;i>=r;i--)
#define show(a,b) For(i,1,n) cerr<<a[i]<<' ';cerr<<'\n';
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 2005;
bool ST;double Tim;

bitset<N> vst;
int a[N][N];
int n;

void Solve(){
	n=rd();For(i,1,n) For(j,1,n) a[i][j]=rd();
	auto swp = [&](auto i){For(j,1,n) swap(a[i][j], a[j][i]);};
	For(i,1,n) For(j,i+1,n){
		if(a[i][j] < a[j][i]) vst[i]=vst[j]=true;
		else if(a[i][j] > a[j][i]){
			if(!vst[i]) swp(i);
			else if(!vst[j]) swp(j);
			vst[i] = vst[j] = true;
		}
	}For(i,1,n){For(j,1,n) write(a[i][j]),putchar(' ');putchar('\n');}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("matrix.in","r",stdin);
	freopen("matrix.out","w",stdout);
	int Tt=1;Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}

100分

#include<bits/stdc++.h>
#include<vector>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define ROf(i,l,r) for(int i=l;i>=r;i--)
#define show(a,b) For(i,1,n) cerr<<a[i]<<' ';cerr<<'\n';
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 2005;
bool ST;double Tim;

int fa[N<<2];inline int find(int x){
	if(x==fa[x]) return x;
	return fa[x] = find(fa[x]);
}inline void merge(int x,int y){fa[find(x)] = find(y);}

int a[N][N];
int n;

void Solve(){
	n=rd();For(i,1,n) For(j,1,n) a[i][j]=rd();
	iota(fa,fa+2*n+1,0);
	For(i,1,n) For(j,i+1,n){
		if(find(i+n) == find(j) && find(i) == find(j+n)){swap(a[i][j], a[j][i]);continue;}
		if(find(i) == find(j) && find(i+n) == find(j+n)){continue;}
		if(a[i][j] > a[j][i]) merge(i,j+n), merge(j,i+n),swap(a[i][j], a[j][i]);
		else if(a[i][j] < a[j][i]) merge(i,j), merge(i+n,j+n);
	}For(i,1,n){For(j,1,n) write(a[i][j]),putchar(' ');putchar('\n');}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("matrix.in","r",stdin);
	freopen("matrix.out","w",stdout);
	int Tt=1;Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}