#C241122C. 修建公路

树形dp
题目
发布日期:   2024-11-22
更新日期:   2024-11-22
文章字数:   3.1k
阅读时长:   14 分

#C241122C. 修建公路

标签（Label）

  • 树形dp

网址（Website）

题目详情 - 修建公路 - Super

题解 - 修建公路 - Super

题目（Problem）

输入数据 1

11 3
1 2 5
2 3 3
2 6 5
3 4 4
3 5 2
1 7 6
7 8 4
7 9 5
1 10 1
10 11 1

输出数据 1

28
28
28
32
30
32
28
32
32
29
30

【样例1解释】

例如对于 $r=1$ 的情况，当 $x_1=4$，$x_2=6$，$x_3=9$ 时国王需要修建代价之和为 $28$ 的公路，且可以证明不会有代价更大的情况。

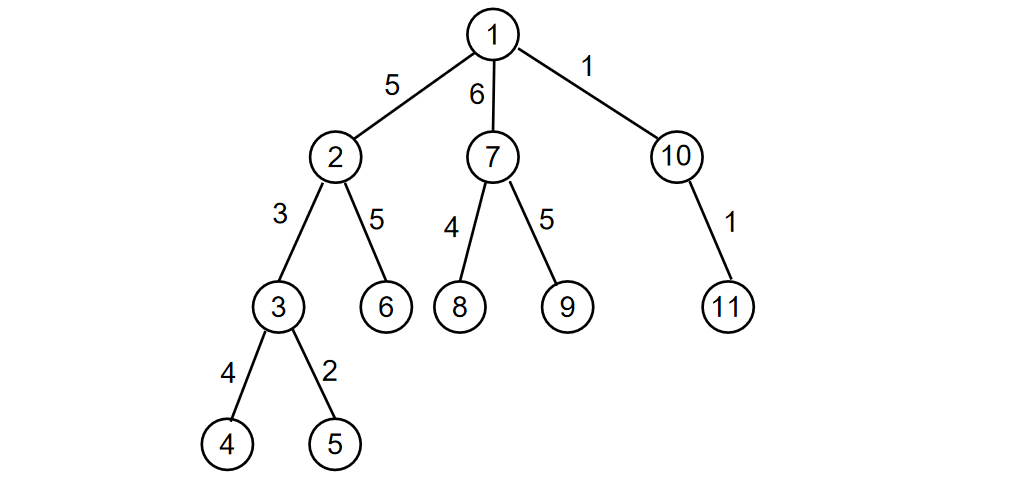
样例2

见选手目录下的 $build/build2.in$ 与 $build/build2.ans$。

该样例满足测试点 $3\sim5$ 的限制。

样例3

见选手目录下的 $build/build3.in$ 与 $build/build3.ans$。

该样例满足测试点 $6\sim9$ 的限制。

样例4

见选手目录下的 $build/build4.in$ 与 $build/build4.ans$。

该样例满足测试点 $10\sim14$ 的限制。

样例5

见选手目录下的 $build/build5.in$ 与 $build/build5.ans$。

该样例满足测试点 $15\sim18$ 的限制。

样例6

见选手目录下的 $build/build6.in$ 与 $build/build6.ans$。

该样例满足测试点 $19\sim25$ 的限制。

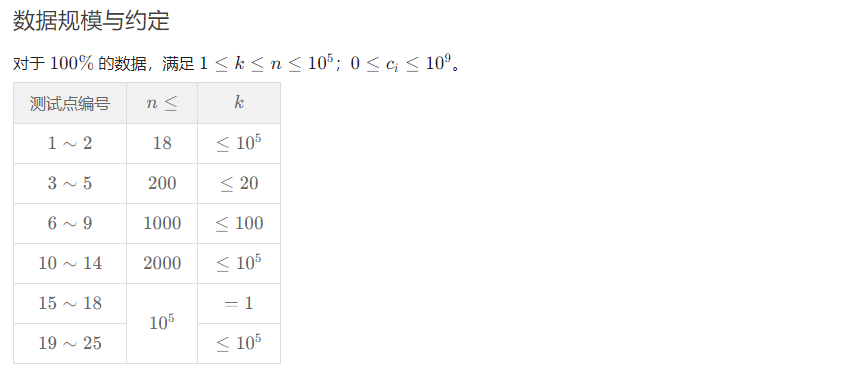
题解（Solution）

56分

非常容易想到先处理一个根的情况，然后就是换根 $\text{dp}$ 。

性质1：选儿子为终点的贡献一定比选其父亲的贡献大，那选儿子一定更好，因此只用考虑选叶子。

叶子的贡献算完了，肯定是再选完的叶子里面再选贡献最大的叶子，这是明显的贪心，而此时新增的贡献就是没有计算过的路径的长度。

类似长链剖分的想法，因为肯定选叶子节点，算出每个叶子的贡献，并且计算出每个叶子到其对应的链顶的边权，排序，取前 $\min(k,n)$ 个即可。

对于每个根算一遍时间复杂度是 $O(n^2\log n)$ ，可以拿一半的分。

100分

考虑换根：

令这两个根的边权为 $v$ 。

分类讨论：

  • 如果新根在最长链上，最后的变化相当于把到原根的最长链贡献 $- v$， 次长链 $+ v$ 。
  • 如果新根不在最长链上 ，最后的变化就是新根子树内的最长链 $- v$， 原根最长链 $+ v$ 。

说白了就是经过新根的最长链 $-v$ ， 经过原根且不经过新根的最长链 $+ v$ 。

只有两条链会因此而变化。

对每个点维护一个不同子树上传来的链的长度最大值和次大值，转移只需要维护一下就好了。

那问题变为了有一串序列，每次会修改其中的两个值，对于每次询问，求出前k大的数的和。

要记录前 $k$ 个的值，暴力还是 $O(k)$ 的，那怎么快速维护前k个呢？最开始可以直接 $O(n\log n)$ 处理，加入贡献，用 $\texttt{multiset}$ 可以做到删除和加入。直接维护两个 $\texttt{multiset}$ ，一个记录前 $k$ 个（记为 $set1$ ），一个记录剩下的（记为 $set2$ ）：

  • 每加入一个数先和第一个 $\texttt{multiset}$ 最小值作比较，考虑加入到哪个集合。加入 $set1$ 就弹一个给 $set2$ ，维护答案，加入 $set2$ 就不用维护答案。

  • 每删除一个数，在两个集合里面找。删的是 $set1$ 就从 $set2$ 里面掏一个最大的过来，维护答案，否则直接删掉 $set2$ 里面的就好了 。

纠错记录：

  1. $\texttt{multiset}$ 的在子节点改变后忘记还原了；根自己也算一条链，不要忽略了。
  2. 这tm谁边权有零啊？ 导致我的 dis[x] < dis[y]+v 会把重儿子判掉，而且后面的 top[i] 会因为初始值是 $0$ 判 $\text{RE}$ 。
  3. 由于我只加了叶子，因此两个 $\texttt{multiset}$ 的总 $siz$ 一定是叶子的个数个，但是由于根也可能是其他子树的叶子，忽略掉根的 $0$ ，在 $\texttt{multiset}$ 里面会删到空的而被判 $\text{RE}$ 。

时间复杂度： $O(n\log n)$ 。

ps：看不懂题解去看代码。

hack数据1
6 1
2 1 2
3 2 0
4 2 5
5 3 1
6 5 1
7
5
5
7
6
7
hack数据2
6 4
2 1 2
3 1 0
4 1 5
5 2 5
6 5 3
15
15
15
15
15
15
出题者题解

代码（Code）

56分
#include<bits/stdc++.h>
#include<vector>
#include<queue>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define ROf(i,l,r) for(int i=l;i>=r;i--)
#define show(a) For(o,1,n) cerr<<a[o]<<' ';cerr<<'\n';
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 2005;
bool ST;double Tim;

vector<P> ft[N];
int n,k,as[N];

int dis[N],son[N];
bitset<N> top;
void dfs_son(int x,int F){
	dis[x] = 0, son[x] = 0;
	for(auto p:ft[x]){
		int y,v;tie(y,v)=p;
		if(y==F) continue;
		dfs_son(y,x);
		if(dis[x] < dis[y]+v){
			dis[x] = dis[y]+v;
			son[x] = y;
		}
	}
	for(auto p:ft[x]){
		int y = p.x, v = p.y;
		if(y==F || y==son[x]) continue;
		top[y] = true;
		dis[y] += v;
	}
}

priority_queue<int> q;
void Solve(){
	n=rd(),k=rd();For(i,1,n-1){
		int x=rd(),y=rd(),w=rd();
		ft[x].emplace_back(y,w);
		ft[y].emplace_back(x,w);
	}
	For(i,1,n){
		top[i] = true;
		dfs_son(i,0);
		
		for(int j=top._Find_first();j<=n;j=top._Find_next(j)){
			q.emplace(dis[j]);
		}int cnt=k;
		while(q.size() && cnt--) as[i]+=q.top(),q.pop();
		
		while(q.size()) q.pop();
		top.reset();
	}
	For(i,1,n) write(as[i]), putchar('\n');
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("build.in","r",stdin);
	freopen("build.out","w",stdout);
	int Tt=1;Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}
100分
#include<bits/stdc++.h>
#include<vector>
#include<set>
#include<queue>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define ROf(i,l,r) for(int i=l;i>=r;i--)
#define show(a) For(o,1,n) cerr<<a[o]<<' ';cerr<<'\n';
using namespace std;
#define P pair<int,int>
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar(x+'0');
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 1012345;
bool ST;double Tim;

/*
换根dp lca 

贪心：找到到根的最长路，暴力更新路径，时间复杂度 O(n^2logn) 甚至到 O(n^3logn) 

如果能选父亲是贡献最大，那父亲的儿子一定更好，因此选叶子 
类似长链剖分的想法，算出每个点的贡献，最后肯定会选叶子节点，干脆只让叶子节点有贡献，并且计算出每个叶子到其对应的链顶的边权，排序，取前min(k,n)个即可
对于每个根算一遍时间复杂度是O(n^2logn)的 可以拿一半的分。
后面应该是换根。

ps：最后的点只能随机，而且应该很水，可能最多 log 个叶子
想起来之前有一个记录到根长为k的路径的点的个数的题，就是用长链剖分做
这里有边权，长链剖分会不会伪啊？如果要跳节点的话复杂度肯定伪，但不确定会不会被卡，但是求答案不需要这个 
（挂一个点分治） 
那就考虑换根：
令这两个根的边权为v 
新的根只有长链会变小 v ，其他的答案不变；
原来根的子树答案不变，只有除去新根对答案的贡献后的长链长度会 + v 

分类讨论：
如果新根在最长链上，最后的变化相当于到原根的最长链 - v， 次长链 + v 
如果新根不在最长链上 ，最后的变化就是新根子树内的最长链 - v， 原根最长链 + v

说白了就是经过新根的最长链 - v， 经过原根且不经过新根的最长链 + v
只有两条链会因此而变化 

对每个点维护一个不同子树上传来的最大值和次大值 ？
使用set维护？ 那怎么维护答案？要记录前 k 个的值，暴力还是 O(k) 的 
我先打个暴力 
...
如何判断当前根是不是最长链？
记录一个次大值 cd ，保证和最大值的子树不一样 
考虑更新dis和cd
最后怎么快速维护前k个?
问题变为了有一串序列，每次会修改其中的两个值，对于每次询问，求出前k大的数的和
最开始可以直接 O(nlogn) 处理，用set可以做到删除和加入。
直接维护两个 set 一个记录前 k 个，一个记录其他
每加入一个数先和第一个作比较，在考虑加入到哪个集合。加入第一个就弹一个给set2，维护答案，加入第二个就不管 
每删除一个数，在两个集合里面找。删的是set1就从set2里面掏一个过来，维护答案，否则直接删掉就好了 

有个特殊情况，就是这棵树的叶子一共才k个不到，那直接就是最后的答案，或者维护的时候判断set2是否为空 

纠错记录：
0.（考试时）set的变化忘记还原了，挂了 ; 根也有一条链，判掉了，直接强制加上 
1.这tm谁边权有零啊？ 导致我的 (dis[x] < dis[y]+v) 会把重儿子判掉，而且后面的 top[i] 会因为初始值是0判RE
2.由于我只加了有效的链，因此两个set的siz一定是叶子的个数个，但是由于根也可能是其他子树的叶子，忽略掉根的0的贡献会RE
*/

vector<P> ft[N];
int n,k,as[N];

int dis[N],cd[N],son[N];
int top[N];
void dfs_son(int x,int F){
	for(auto p:ft[x]){
		int y,v;tie(y,v)=p;
		if(y==F) continue;
		dfs_son(y,x);
		if(dis[x] <= dis[y]+v){
			cd[x] = dis[x];
			dis[x] = dis[y]+v;
			son[x] = y;
		}else cd[x] = max(cd[x], dis[y]+v); 
	}
	for(auto p:ft[x]){
		int y = p.x, v = p.y;
		if(y==F || y==son[x]) continue;
		top[y]=v;
	}
}

multiset<int,greater<int>> s1,s2;
int ans;
inline void ins(int x){
	if((int)s1.size()<k || x>*prev(s1.end())){
		s1.emplace(x), ans += x;
	}else s2.emplace(x);
	while((int)s1.size() > k){
		ans -= *prev(s1.end());
		s2.emplace(*prev(s1.end()));
		s1.erase(prev(s1.end()));
	}
}
inline void del(int x){
	auto p = s1.find(x);
	if(p==s1.end()) s2.erase(s2.find(x));
	else ans-=x, s1.erase(p);
	while(s2.size() && (int)s1.size() < k){
		ans += *s2.begin();
		s1.emplace(*s2.begin());
		s2.erase(s2.begin());
	}
}

void dfs_root(int x,int F){
	for(auto p:ft[x]){
		int y=p.x,v=p.y;if(y==F) continue;
		if(y==son[x]){//这个肯定是最长链
			int a=dis[x],b=dis[y],c=cd[x],d=cd[x]+v;
			del(dis[x]), ins(dis[y]);
			del(cd[x]), ins(cd[x]+v);
			as[y] = ans;
			
			//先考虑父亲组成的新链 
			if(dis[y] <= cd[x]+v){//这个时候肯定不在一棵子树内 
				cd[y] = dis[y];
				dis[y] = cd[x]+v;
				son[y] = x;
			}else cd[y] = max(cd[y], cd[x]+v);
			
			dfs_root(y,x);
			
			ins(a), del(b);
			ins(c), del(d);
			//自己的dis已经考虑过自己变短的新链了，就不用考虑了 
		}else{
			int a=dis[y]+v,b=dis[y],c=dis[x],d=dis[x]+v;
			del(dis[y]+v), ins(dis[y]);
			del(dis[x]), ins(dis[x]+v);
			as[y] = ans;
			
			//先考虑父亲组成的新链 
			if(dis[y] <= dis[x]+v){
				cd[y] = dis[y];
				dis[y] = dis[x]+v;
				son[y] = x;
			}else cd[y] = max(cd[y], dis[x]+v);
			
			dfs_root(y,x);
			
			ins(a), del(b);
			ins(c), del(d);
		}
	}
}

priority_queue<int> q;
void Solve(){
	n=rd(),k=rd();For(i,1,n-1){
		int x=rd(),y=rd(),w=rd();
		ft[x].emplace_back(y,w);
		ft[y].emplace_back(x,w);
	}fill(top,top+n+1,-1);
	dfs_son(1,0), ins(dis[1]);
	For(i,2,n) if(~top[i]) ins(dis[i]+top[i]);
	if(ft[1].size()==1) ins(0);
	as[1] = ans;
	dfs_root(1,0);
	For(i,1,n) write(as[i]), putchar('\n');
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("build.in","r",stdin);
	freopen("build.out","w",stdout);
	int Tt=1;Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}
文章作者: WolfDeer
文章链接: https://wolfdeer62456.github.iohttps://wolfdeer62456.github.io/2024/11/22/C241122C-%E4%BF%AE%E5%BB%BA%E5%85%AC%E8%B7%AF/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 WolfDeer !
树形dp
赏
  目录