#C241125B. 染色

标签（Label）

动态规划
矩阵
线段树

网址（Website）

题目详情 - 染色 - Super

题解 - 染色 - Super

题目（Problem）

输入数据 1

输出数据 1

9
9
1

【样例1解释】

询问进行解密后为：

对于原画布的答案，我们可以选择 $1,3$ 小格，并将 $2$ 小格的颜色变为 $2$，这样整个画布的美观度为 $4+4+1=9$。

样例2

见选手目录下的 $paint/paint2.in$ 与 $paint/paint2.ans$。

样例3

见选手目录下的 $paint/paint3.in$ 与 $paint/paint3.ans$。

该样例数据满足子任务 3 的限制。

样例4

见选手目录下的 $paint/paint4.in$ 与 $paint/paint4.ans$。

该样例数据满足子任务 5 的限制。

样例5

见选手目录下的 $paint/paint5.in$ 与 $paint/paint5.ans$。

该样例数据满足子任务 6 的限制。

样例6

见选手目录下的 $paint/paint6.in$ 与 $paint/paint6.ans$。

该样例数据满足子任务 8 的限制。

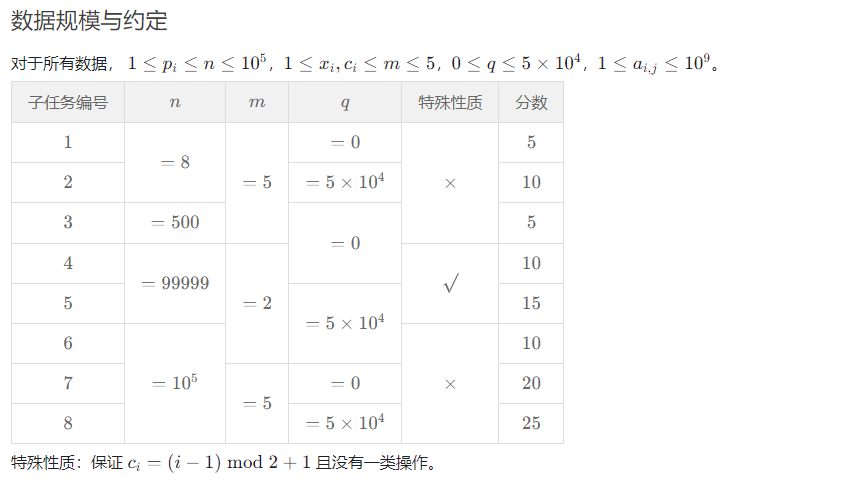
题解（Solution）

这个出题者题解有问题：

$f_{i,j}$ 的定义应该是当前位置 $i$ 染 $j$ 颜色是，$1\sim {i-1}$ 位置的美观度；
额外增加的转移应该是 $f_{i,c_i}+a_{i,c_i}\to f_{i+1,0}$ 和 $f_{i,0}+a_{i,c_i}\to f_{i+1,c_{i+1}}$ ；
最后的时间复杂度是 $O(q\log n\times 36)$ 。

其他的没有理解到，特别是如何转化到矩阵上面的，感觉一点思路都没有，好像有一个 $(\min+)$ 矩阵的玩意，不会。

出题者题解

代码（Code）

50分

#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
#define show(a) For(i,1,n) cerr<<a[i]<<' ';cerr<<' ';
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar('0'+x);
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 1012345;
bool ST;

/*
单点修，区间查
考虑dp，每次修改当且仅当将[lsti+1,i-1]染成相同颜色后是美观度变大，
且一定不会跨相同颜色操作，要么等效，要么不优

时间复杂度 O(nq)，得分50pts
*/

int a[N][6],b[N][6];
int n,m,q,c[N];

int lst[6], f[N];
inline int ask(int col, int l, int r){return b[r][col] - b[l-1][col];}
int calc(int l,int r){
	memset(lst,0,sizeof lst), f[l-1]=0;
	For(i,l,r){
		f[i] = f[i-1]+a[i][c[i]];
		if(lst[c[i]]){
			f[i] = max(f[i], f[lst[c[i]]] + ask(c[i], lst[c[i]]+1, i));
		}lst[c[i]] = i;
	}return f[r];
}

void Solve(){
	n=rd(), m=rd(), q=rd(); For(i,1,n) c[i]=rd();
	For(i,1,n) For(j,1,m) a[i][j]=rd();
	For(j,1,m) For(i,1,n) b[i][j]=a[i][j]+b[i-1][j];//相同颜色前缀和 
	
	int ans = calc(1,n);
	write(ans), putchar('\n');
	
	while(q--){
		int op=rd(), l=rd()^ans, r=rd()^ans;
		if(op==1){
			c[l] = r;
		}else{
			write(ans = calc(l,r)), putchar('\n'); 
		}
	}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("paint.in","r",stdin);
	freopen("paint.out","w",stdout);
	int Tt=1;double Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}

100分

#include<bits/stdc++.h>
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rof(i,l,r) for(int i=l;i>=r;i--)
#define show(a) For(i,1,n) cerr<<a[i]<<' ';cerr<<' ';
using namespace std;
#define P pair<int,int> 
#define int long long
#define x first
#define y second
inline int rd(){
	char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48;
	while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x;
}template<typename G>
void write(G x){
	if(x<0) putchar('-'),write(-x);
	else if(x<=9) putchar('0'+x);
	else write(x/10), putchar(x%10+'0');
}constexpr int inf = 0x3f3f3f3f3f3f3f3f;
constexpr int N = 201234;
bool ST;

int n,m,q,ans,c[N],a[N][6];

struct mtx{
	int n,m,a[6][6];
	void resize(int x,int y){
		tie(n,m) = tie(x,y);memset(a,-0x3f,sizeof a);}
	mtx(int n=0,int m=0){resize(n,m);}
};

mtx operator+(const mtx &x, const mtx &y){
	mtx res(x.n, y.m);For(i,0,x.n) For(j,0,y.m) For(k,0,x.m){
		res.a[i][j] = max(res.a[i][j], x.a[i][k]+y.a[k][j]);
	}return res;
}

mtx getmtx(int x){
	mtx res(m,m); For(i,1,m) res.a[i][i] = a[x][i];
	res.a[0][0] = res.a[0][c[x]] = res.a[c[x]][0] = a[x][c[x]];
	return res;
}

namespace tree{
	#define mid ((l+r)>>1)
	#define ls (p<<1)
	#define rs (p<<1|1)
	mtx tr[N<<2|3];	void pushup(int p){tr[p]=tr[ls]+tr[rs];}
	void build(int p,int l,int r){
		if(l == r) return tr[p] = getmtx(l), void(); 
		build(ls,l,mid),build(rs,mid+1,r),pushup(p);
	}
	void update(int p,int l,int r,int x){
		if(l==r) return tr[p] = getmtx(l), void();
		x <= mid ? update(ls,l,mid,x) : update(rs,mid+1,r,x);
		pushup(p); 
	}
	void ask(int p,int l,int r,int L,int R,mtx &res){
		if(L<=l && r<=R) return res = res+tr[p], void();
		if(L<=mid) ask(ls,l,mid,L,R,res);
		if(R>mid) ask(rs,mid+1,r,L,R,res);
	}
}

void Solve(){
	n=rd(), m=rd(), q=rd(); For(i,1,n) c[i]=rd();
	For(i,1,n) For(j,1,m) a[i][j]=rd();
	tree::build(1,1,n);
	write(ans = tree::tr[1].a[0][0]), putchar('\n');
	while(q--){
		int op=rd(), l=rd()^ans, r=rd()^ans;
		if(op == 1) c[l]=r, tree::update(1,1,n,l);
		if(op == 2){
			mtx res(0,m); res.a[0][0] = 0;
			tree::ask(1,1,n,l,r,res);
			write(ans = res.a[0][0]), putchar('\n');
		}
	}
}

bool ED;
signed main(){
	cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n";
	freopen("paint.in","r",stdin);
	freopen("paint.out","w",stdout);
	int Tt=1;double Tim = clock();
	while(Tt--) Solve();
	return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0;
}