#C241128B. 梦相遇
标签(Label)
- 二分答案
- 深搜
网址(Website)
题目(Problem)


输入数据 1
1 4
3 3 1
3 3
3 5 4
1 1
1 2
1 5
3 3
3 5 5
1 1
1 2
1 5
2 4
3 3
6 6 6
1 1
1 2
2 1
5 6
6 5
6 6输出数据 1
2
1
-1
3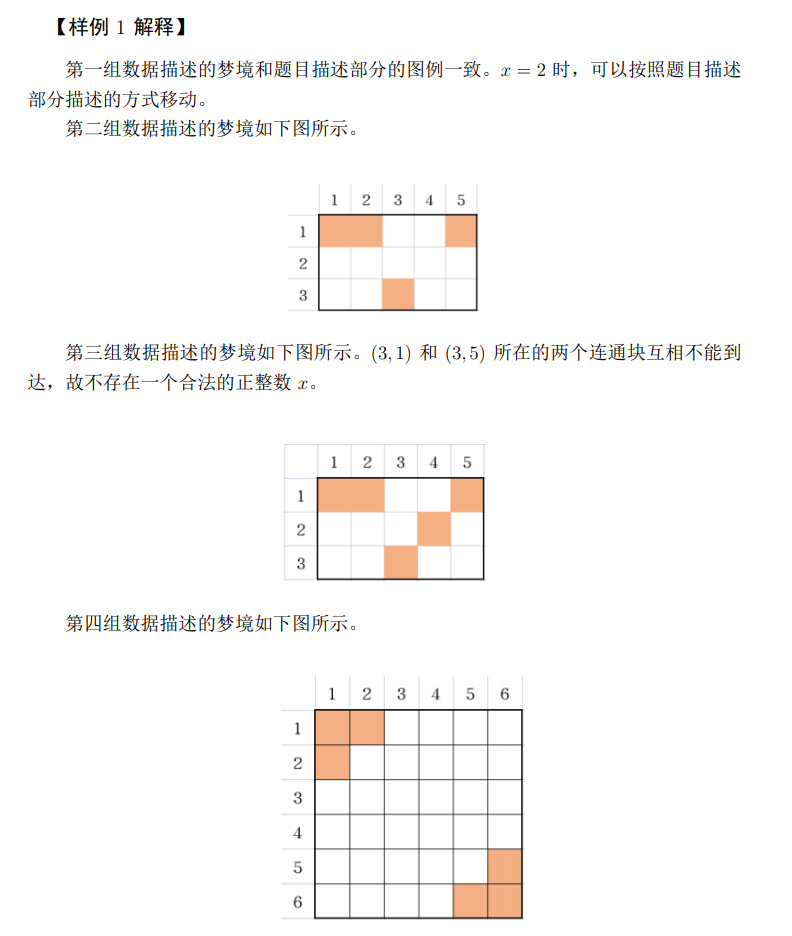
样例 2
见选手目录下的 $meet/meet2.in$ 与 $meet/meet2.ans$。
该样例满足测试点 $9, 10$ 的限制。
样例 3
见选手目录下的 $meet/meet3.in$ 与 $meet/meet3.ans$。
该样例满足测试点 $1 \sim 3$ 的限制。
样例 4
见选手目录下的 $meet/meet4.in$ 与 $meet/meet4.ans$。
该样例满足测试点 $8$ 的限制。
样例 5
见选手目录下的 $meet/meet5.in$ 与 $meet/meet5.ans$。
该样例满足测试点 $12$ 的限制。
样例 6
见选手目录下的 $meet/meet6.in$ 与 $meet/meet6.ans$。
该样例满足测试点 $18 \sim 20$ 的限制。

题解(Solution)
由于求得是最大,很容易发现答案单调性,直接二分答案。
接下来考虑的就是在 $O(nm)$ 时间内计算出当前的 $mid$ 能否满足条件。
先考虑怎么放矩阵,很明显可以直接记录二维前缀和,然后求出区间内是否有禁行区。
后面考虑直接 $\text{dfs}$ 遍历,怎么记录这个矩阵呢?本来想的是记录四个角,其实因为长宽已知,只需要记录左上角就好了,遍历的时候判断四个角是否满足条件即可。
这里提几个需要注意的点,因为题目的限制是 $n\times m\le3\times10^6$ ,因此我使用的是指针来表示矩阵,原来的代码是计算的每一行 $m$ 个元素,但是发现我使用矩阵的时候需要用到诸如 $(n+1,1),(1,m+1),(0,0)$ 这些位置,因为一行只有 $m$ 个元素,因此访问的时候总是会访问到前面的位置,导致最后答案出错。因此,一行至少要设成 $(m+2)$ 个元素,防止访问的时候炸掉。我可是多打了 $\text{1.5k}$ 的代码才发现这个问题。
正确的打法应该是这样:
struct Wolf{
int v[N];
int *operator[](const int x){return v+x*(m+2);}
void clear(int n,int m){memset(v,0,(n+2)*(m+2)*sizeof(v[0]));}
}c,d;后面又调了几十分钟的代码,才发现是求前缀和求错了,原来我用的是 $x_1,y_1,x_2,y_2$ ,后面害怕用到关键字又改成了 $x,y,i,j$ ,结果恰巧发现了这个问题——我把 -c[x1-1][y2] 写成了 -c[x1-1][y1] ,换成 $i,j$ 之后就很容易发现 -c[i-1][j] 不对,之后还是要用有区分度的变量,要不然容易看错,还找不到。
(所以就不理解为什么要用 $u,v$ 作为点,这两个东西是最容易看错的)
时间复杂度: $O(S\log S)$ 。
出题者题解

代码(Code)
100分
#include<bits/stdc++.h> #include<vector> #define For(i,l,r) for(int i=l;i<=r;i++) #define Rof(i,l,r) for(int i=l;i>=r;i--) #define show(a,n) {For(o,1,n) cerr<<a[o]<<' ';cerr<<'\n';} using namespace std; #define P pair<int,int> #define int long long #define x first #define y second #define in(x,l,r) (l<=x && x<=r) inline int rd(){ char c;bool f=false;while(!isdigit(c=getchar()))f=c=='-';int x=c^48; while(isdigit(c=getchar())){x=(((x<<2)+x)<<1)+(c^48);}return f?-x:x; }template<typename G> void write(G x){ if(x<0) putchar('-'),write(-x); else if(x<=9) putchar('0'+x); else write(x/10), putchar('0'+x%10); }constexpr int inf = 0x3f3f3f3f3f3f3f3fll; constexpr int N = 10123456; bool ST;int Tt,tid; /* 答案单调性->二分答案 转换为知道矩形大小,如何在O(nm)时间内得出是否可行 O(nm)放矩阵?直接判断是否能放 记录矩阵四个角,dfs搜索上下左右,除去最开始覆盖了x*x的方格,还要覆盖n*m-x*x-ban个方格。 处理已经走过的位置的问题,由于形状固定只需要记录左上角的点即可 如何判断是否走完了所有的点?每次走的时候记录前缀和表示该段被覆盖, 最后O(nm)遍历全图求前缀和,如果有位置没有被禁用且前缀和为0,那么不行 */ int n,m,k; struct Wolf{ int v[N]; int *operator[](const int x){return v+x*(m+2);} void clear(int n,int m){memset(v,0,(n+2)*(m+2)*sizeof(v[0]));} }c,d; inline int ask(int i,int j,int x,int y){ return c[x][y]-c[x][j-1]-c[i-1][y]+c[i-1][j-1]; } struct Deer{ bool v[N]; bool *operator[](const int x){return v+x*(m+2);} void clear(int n,int m){memset(v,0,(n+2)*(m+2)*sizeof(v[0]));} }a,vst; int dx[] = {0,0,1,-1}; int dy[] = {1,-1,0,0}; void dfs(int x,int y,int md){ d[x][y]++, d[x+md][y+md]++; d[x][y+md]--, d[x+md][y]--; vst[x][y] = true; For(k,0,3){ int i=x+dx[k], j=y+dy[k]; if(!vst[i][j] && in(i,1,n) && in(j,1,m) && in(i+md-1,1,n) && in(j+md-1,1,m) && !ask(i,j,i+md-1,j+md-1)) //如果没有走过 且 矩阵在合理范围内 且 没有覆盖禁行点 dfs(i,j,md); } } bool check(int mid){ vst.clear(n,m), d.clear(n,m); bool flag = true; for(int i=1;i<=n-mid+1&&flag;i++){ for(int j=1;j<=m-mid+1&&flag;j++){ if(ask(i,j,i+mid-1,j+mid-1)==0)//如果中间没有禁行区 dfs(i,j,mid),flag=false; }}if(flag) return false; For(i,1,n) For(j,1,m){ d[i][j] += d[i][j-1]+d[i-1][j]-d[i-1][j-1]; if(!d[i][j] && !a[i][j]) return false; }return true; } void Solve(){ a.clear(n,m), c.clear(n,m); n=rd(),m=rd(),k=rd();For(i,1,k) a[rd()][rd()] = 1; For(i,1,n) For(j,1,m) c[i][j]=c[i-1][j]+c[i][j-1]-c[i-1][j-1]+a[i][j]; int l=1, r=min(n,m), mid, res=-1; while(l<=r){ mid = (l+r)>>1; if(check(mid)) l=mid+1, res=mid; else r=mid-1; } if(~res) write(res), putchar('\n'); else write(-1), putchar('\n'); } bool ED; signed main(){ cerr<<abs(&ST-&ED)/1024./1024.<<"MB\n"; freopen("meet.in","r",stdin); freopen("meet.out","w",stdout); tid=rd(),Tt=rd();double Tim=clock(); while(Tt--) Solve(); return cerr<<"TIME:"<<(clock()-Tim)/CLOCKS_PER_SEC,0; }



