2024.05.18 考试总结

附件：见 Problem.pdf 和 Solution.pdf.

T1： 构造一个简单无向图，使得 $1$ 号点与 $2$ 号点之间的最短路数量严格等于 $k$ ，且点数尽量少。

$\qquad$这道题其实就是一道很简单的思考题，其中 $k$ 给了 $1e9$ ，所以自然会联想到 $log_2k$ 的处理方式，于是题目就变得简单了：

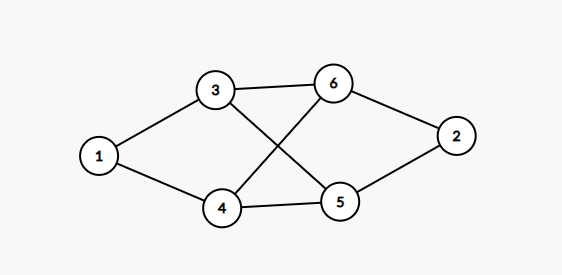
$\qquad$看这两张图，可见此时的路径数量为 $2^s$ ，其中 $s$ 表示分叉路的组数，这样，我们就能在只用 $62$ 个点的情况下（包括首尾）构造出一个 $2^{30}$ 的的路径条数，而我们有知道，对于每个数 $x\in N$ ，$x$ 一定可以拆分为 $2$ 的次幂的和的形式（例如 $7 = 2^2+2^1+2^0$ 、$9=2^3+2^0$），所以我们可以再用大约 $30$ 个点来构造一条“外路”（原来的就称其为“内路”），如图所示：

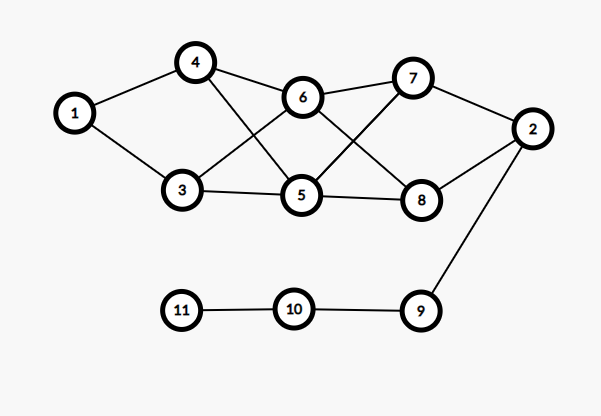
$\qquad$如此构造有什么用处呢？不难发现，当我们需要构造 $11$ 条路径时，由于 $11=2^3+2^1+2^0$ 所以在已有的 $2^3$ 条路径上，我们可以这样连：

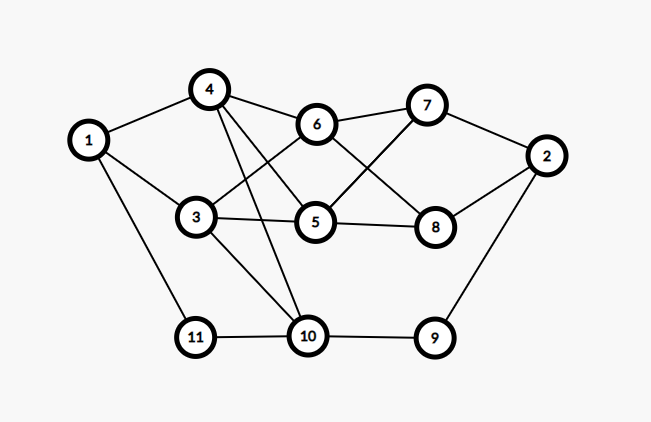
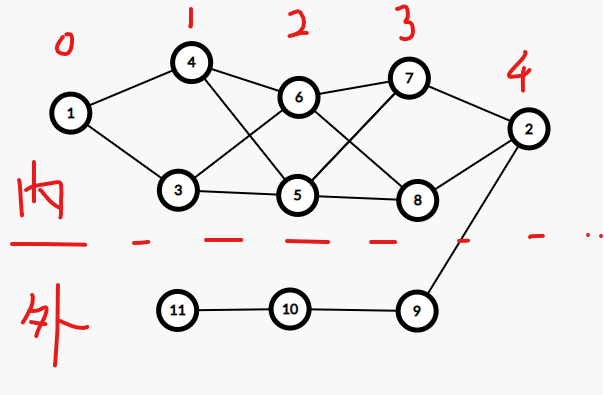
$\qquad$这样就轻易的构造出了一张 $11$ 条路径的图了，具体的方法是：若我们给每一列标一个号当需要 $2^i$ 条路径时，只需要将第 $i$ 列的“内路”和第 $i+1$ 列的外路连接就好了。注意，不用连 $2$ 的最多路径的（就是 $11$ 里面的 $2^3$ ），因为原来的图已经有那么多条路经了。

$\qquad$标号方式见图：

$\qquad$当时想这道题想了很久，后来才发现从一开始就少想了几种情况，导致耗费了大量的思考时间。

T3

$\qquad$这道题没有想到的是： $Num(p,q)$ 的阶乘中有多少个 $p$ 可以用 $f(p,q)=\sum_{i=1,p^i\le N}^{q}\lfloor \frac{N}{p^i} \rfloor $ 表示，再联系到 $Num(p,q)=\sum_{i=0}^q D_i* p^i$ ，就知道该倒叙求值了。这里还有两个思维方式：1.由于 $Num(p,q)$ 的形式像极了 $p$ 的进制数，所以不妨设 $p=10$ ，用十进制来理解并推导式子，在推广到其他的 $p$ ；2.由于题目给了 $gcd(p-1,n)=1$ 的条件，所以可以在求值的过程中直接模 $n$ ，结果并不会改变。